Sets
Relations
Correspondences
Ordered Sets
Lattices
Graphs
Powersets
Binary Strings
Logic
AIA
Greek
Glossary
Abstracts
Argument
Inquiry Cycle
Legal Relations
Presentations
Elicitation
Glossaries
Goals
i*
SCR
Tracing
Design Patterns
Javadoc
Java Packages
Java Types
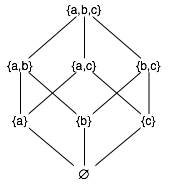
Figure 2
The powerset of {a, b, c},
ordered by ⊆

Figure 1
The integers,
totally ordered
by ≤; a chain
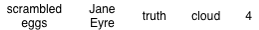
Figure 3
Incomparable items forming an antichain
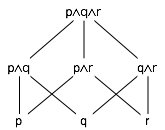
Figure 6
The conjunctions of any of
p, q, and r,
ordered by implication
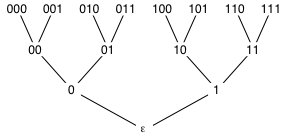
Figure 5
The binary strings no longer than 3,
ordered by the prefix relation ≤
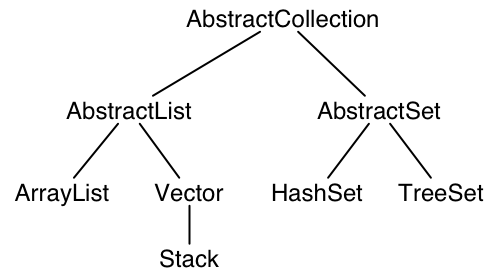
Figure 4
Part of the java.util inheritance structure
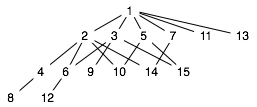
Figure 8
The dual of the ordered set in Figure 7
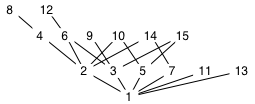
Figure 7
The positive integers to 15,
ordered by the divisibility relation
Let P be a set and ⊑ be a (partial) order on P. Then P and ⊑ form a (partially) ordered set.
If the order is total, so that no two elements of P are incomparable, then the ordered set is a totally ordered set. Totally ordered sets are the ones people are first familiar with. See Figure 1 for an example.
A totally ordered set is also termed a chain.
If the order is partial, so that P has two or more incomparable elements, then the ordered set is a partially ordered set. See Figure 2 for an example.
At the other extreme, if no two elements are comparable unless they are equal, then the ordered set is an antichain. See Figure 3.
On any set, = is an order; this is termed the discrete order on the set. Any set ordered by = forms an antichain.
It is common for people to refer briefly though inaccurately to an ordered set as an order, to a totally ordered set as a total order, and to a partially ordered set as a partial order. It is usually clear by context whether "order" refers literally to an order (an order relation) or by synecdoche to an ordered set.
Examples:
- The integers with ≤ form an ordered set (see Figure 1). ≤ is a total order on the integers, so this ordered set is a chain.
- Any powerset with ⊆ forms an ordered set (see Figure 2). This is a partially ordered set because not all subsets are related by ⊆, for example {a} || {b, r}.
- A set of unrelated items, ordered by =, is the discrete order on that set and forms an antichain (see Figure 3).
- The classes in java.util with the subclass relation form an ordered set (see Figure 4). This set is partially ordered, because not all classes in the set are related by the subclass relations (for example, Vector and HashSet are not related and are thus incomparable: Vector || HashSet).
- A set of binary strings with the prefix relation forms an ordered set (see Figure 5). This is set is partially ordered because not all strings are related by the prefix relation, for example 01 || 10.
- The (non-empty) conjunctions of any of the propositions p, q, and r, ordered by implication, form an ordered set (see Figure 6). In this set, p∧q implies q, but p∧q neither implies nor is implied by q∧r, so p∧q and q∧r are incomparable (p∧q # q∧r) .
- The positive integers N with the divisibility relation form an ordered set. The divisibility relation relates m to n if m divides n, written m | n. Thus 2 | 6, and 3 | 6 but not 4 | 6 (i.e., 4 and 6 are incomparable, written 4 || 6) because 4 does not divide 6. And for any n∈N, 1 | n and n | n. A part of this ordered set is shown in Figure 7.
Duality
Each ordered set P corresponds to another ordered set P∂, the dual of P, defined by: y⊑x in P∂ iff x⊑y in P.
Each statement Φ about P corresponds to a dual statement Φ∂ about P∂. Φ∂ is obtained by replacing each occurrence of ⊑ in Φ by ⊒, and each occurrence of ⊒ in Φ by ⊑. Φ is true about P if and only if Φ∂ is true about P∂. Generalizing, it can be shown that if a statement Φ is true about all ordered sets, then its dual statement Φ∂ is also true. This assertion is the Duality Principle.
Pairs of dual concepts that are defined in terms of ⊑ and ⊒ (such as upper bound and lower bound, below), are also exchanged in dual statements.
Example: Let Q be the ordered set shown in Figure 7, in which ⊑ is the integer divides relation, with the divisor "lower than" the dividend. Then the ordered set of the positive integers to 15 ordered by the converse of divides (now with the divisor considered "higher" than the dividend), is the dual Q∂ of Q. The converse of |, |-1, relates two integers if one divides the other, but unlike | it classifies the numerically-smaller integer as the "higher" one by this relation, so that for this order 2⊑1, for example. Q∂ is shown in Figure 8. In Q, 4⊑8, so we know without looking at Figure 8 that in Q∂, the dual statement 4⊒8 holds in the relation for that ordered set.
Extrema
Let S be an ordered set.
- u∈S is said to be maximal in S iff there is no v∈S such that u≤v. A set may have any number of maximal elements, including zero.
- If u is S's only maximal element, then u is the maximum of S.
- The maximum element u (if it exists) is also called the top of S and is denoted by ⊤.
- Dually, t∈S is said to be minimal in S iff there is no s∈S such that s≤t. A set may have any number of minimal elements, including zero.
- If t is S's only minimal element, then t is the minimum of S.
- The minimum element t (if it exists) is also called the bottom of S and is denoted by ⊥.
Examples:
- p∧q∧r is a maximal element of the set in Figure 6. Since it is the only maximal element, it is the maximum or top.
- The set in Figure 6 has three minimal elements (p, q, and r). It has no minimum (because it has three minimal elements).
- The set of all integers has no maximal or minimal elements (Figure 1). It has no maximum (because it has no maximal elements); similarly, it has no minimum.
Bounds
Upper bounds and LUBs

Figure 5 (again)
The binary strings no longer than 3,
ordered by the prefix relation (with prefix low)
Let S be an ordered set and let E⊆S.
- y∈S is an upper bound of E iff x≤y for every x∈E. E may have no upper bound, one upper bound, or many. Note that y need not be an element of E in order to be an upper bound of E.
- We write Eu to denote the set of all upper bounds of E. Eu may be empty, a singleton, or have many members.
- If Eu
is non-empty and has a minimum element u,
then u is called the
least upper bound (LUB) of E,
written ∨E.
The LUB of E is also called the
supremum or join of E.
In the common case where E consists of exactly two elements s and t, we can also write s∨t (pronounced "the least upper bound of s and t" or "s join t").
Examples, using the ordered set of Figure 5 as S:
- Consider E={01}. E has several upper bounds in S, 01 itself, 010, and 011, so EU={01,010,011}. EU has a minimum element under the prefix relation ≤, and that minimum is 01, so E={01} has a LUB of 01 in S.
- Consider E={00,01}. There is no element of S that is greater than both 00 and 01. E thus has no upper bound in S, and EU is empty. EU has no minimum element under the prefix relation ≤ (because it has no elements at all), so E has no LUB in S.
Lower bounds and GLBs
The dual concept for upper bound is lower bound, and analogous definitions apply.
- z∈S is a lower bound of E iff z≤x for every x∈E. Note that z need not be an element of E in order to be a lower bound of E.
- We write El to denote the set of all lower bounds of E.
- If El
is non-empty and has a maximum element v,
then v is called the greatest lower bound (GLB) of E,
written ∧E.
The GLB of E is also called the
infimum or meet of E.
In the common case where E consists of exactly two elements s and t, we can also write s∧t (pronounced "the greatest lower bound of s and t" or "s meet t").
Examples:
- (Figure 5) 000 ∨ 001 is 00.
- (Figure 3) { scrambled eggs, Jane Eyre } has no GLB because it has no lower bound at all.
Existence of LUBs and GLBs
A LUB (GLB) can fail to exist for either of two reasons:
- There may be no upper (lower) bound at all; Eu (El ) may be empty (for example, the binary strings in Figure 5 and {000, 001}).
- There may be upper (lower) bounds,
but no least upper bound (greatest lower bound).
- There may be two or more minimal upper bounds (maximal lower bounds) that are not comparable, so that neither can be least (greatest) (for example, the divisibility ordering in Figure 7 and {2, 3}); or
- There may be an infinite descending (ascending) chain of upper (lower) bounds, so that none is minimal (maximal) (for example, as in the case of the reals with <).
LUB and GLB synonyms and symbols
The table below gives the several synonyms and symbols related to greatest lower bound and least upper bound.
| Name | Abbrev. | Synonyms | Operator | Goes with ... |
|---|---|---|---|---|
| least upper bound | LUB | supremum, join | ∨ | top ⊤ |
| greatest lower bound | GLB | infimum, meet | ∧ | bottom ⊥ |
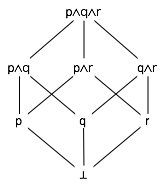
Figure 9.
The ordered set of Figure 6, lifted
Lifting
It is often useful for an ordered set to have a bottom, but not all ordered sets have one (for example, the set in Figure 6). In this case, we can produce a new ordered set with a bottom by adding a (new) least element to the original ordered set. This process is called lifting, and the result of lifting an ordered set P can be called "P lifted", written P⊥.
Example: The non-empty conjunctions of any of p, q, and r, ordered by implication (see Figure 6), has no bottom element. We can lift this set by adding a new element, ⊥, which is implied by all other elements. Here, ⊥ may be thought of as representing the conjunction of 0 propositions. The lifted set is diagrammed in Figure 9. In terms of the knowledge expressed by each conjunction, we may say that a conjunction is an assertion that we know each of its conjuncts is true; thus, for example, p∧r is an assertion that we know p is true and we know r is true. Then ⊥ is an empty assertion, one that does not assert that we know that any of p, q, or r are true.
Diagrams
We have been using diagrams of ordered sets without defining what they mean, relying on the reader's intuition. It is time to confirm that intuition by defining what the diagrams mean.
First we must consider the concept of covering.
For x,y ∈
set P ordered by ≤,
we say x is covered by y
(written
x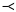 y)
if x<y
and for any z∈P,
x≤z<y
implies x=z.
This means that there is no element of P "between"
x and y.
Equivalently,
we say
y covers x.
y)
if x<y
and for any z∈P,
x≤z<y
implies x=z.
This means that there is no element of P "between"
x and y.
Equivalently,
we say
y covers x.
A diagram (or Hasse diagram) of an ordered set is a graph in which
- each node corresponds to an element of the set,
- each edge corresponds to a covering relation between the nodes it connects, and
- if
x
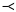 y,
then the node for x is drawn in a lower position than the node for y.
y,
then the node for x is drawn in a lower position than the node for y.
Thus we see that in interpreting diagrams, it does not matter whether one node is above or below another unless there is a monotonic path between them; and that if there is a monotonic path from y through one or more nodes down to x, there is no separate edge directly from y to x.
Examples in Figure 9:
- p∧q
covers p
(because no other node is between them).
We may also write
p
is covered by
p∧q
or
p
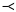 p∧q.
p∧q.
- The figure indicates that p∧q∧r implies q. Even though there is no line directly from p∧q∧r to q, we know this because there is a monotonically-descending path from p∧q∧r to q.
- There are non-monotonic paths from p∧q to q∧r (for example, down to q and back up), but this doesn't mean that p∧q implies q∧r, because none of the paths are monotonically descending. In fact, p∧q || q∧r.
Other examples:
- In Figure 7, 5 is below 9 but this doesn't mean that 5 | 9 because there is no monotonic path between them. In fact, 5 || 9.
Isomorphisms on ordered sets
The ordering of two sets may be the same even if the two sets are different. Two ordered sets P and Q are order-isomorphic, written P ≅Q, if there is a mapping φ from P onto Q such that x ≤y in P if and only if φ(x) ≤φ(y) in Q. Then φ is called an order-isomorphism on the two sets. In discussing ordered sets, we often simply say P and Q are isomorphic or φ is an isomorphism.
It can be shown that two ordered sets are order-isomorphic if and only if they can be drawn with identical diagrams.

Figure 2 (again)
℘{a, b, c}, ordered by ⊆
Example: The powerset of {a, b, c} ordered by the subset relation (Figure 2), and the conjunctions of any of a, b, and c ordered by implication and lifted by the addition of ⊥ (Figure 9), are isomorphic. The isomorphism between them is given in the table below.
| x∈P | φ(x)∈Q |
|---|---|
| {a, b, c} | a∧b∧c |
| {a, b} | a∧b |
| {a, c} | a∧c |
| {b, c} | b∧c |
| {a} | a |
| {b} | b |
| {c} | c |
| ∅ | ⊥ |
From this isomorphism, we can see that because {a, b, c} ⊇{b, c}, we know that φ({a, b, c}) implies φ({b, c}) or (written in terms of Q) a∧b∧c implies b∧c.

Figure 6 (again)
Q: Conjunctions ordered by implication
Figure 3 (again)
P: Incomparable items forming an antichain
Constructing an ordered set from another ordered set
The disjoint union of two disjoint ordered sets P and Q,
written
P Q,
is the union of P and Q,
with P's elements ordered as in P
and Q's elements ordered as in Q,
and each element of P incomparable with each element of Q.
The diagram of
P
Q,
is the union of P and Q,
with P's elements ordered as in P
and Q's elements ordered as in Q,
and each element of P incomparable with each element of Q.
The diagram of
P Q
consists of P's diagram beside Q's diagram,
with no connection between them.
Q
consists of P's diagram beside Q's diagram,
with no connection between them.
The linear sum of two disjoint ordered sets P and Q, written P⊕Q, is the union of P and Q, with P's elements ordered as in P and Q's elements ordered as in Q, and x≤y for each x∈P and y∈Q. The diagram of P⊕Q consists of Q's diagram above P's diagram, with an edge between each minimal element of Q and each maximal element of P.

Figure 10.
Disjoint union
(P Q)
of Figures 3 (P) and 6 (Q)
Q)
of Figures 3 (P) and 6 (Q)
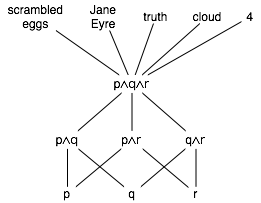
Figure 12. Linear sum (Q⊕P) of Figs. 6 (Q) and 3 (P)
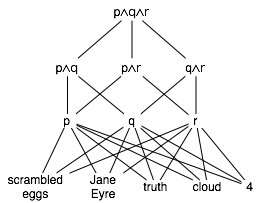
Figure 11. Linear sum (P⊕Q) of Figs. 3 (P) and 6 (Q)
Examples, using the ordered sets P from Figure 3 and Q from Figure 6:
-
Figure 10 shows the disjoint union of
P and Q,
written
P
 Q.
In the disjoint union,
every elements from one set is incomparable to all elements in the other,
but each set retains its own ordering.
Q.
In the disjoint union,
every elements from one set is incomparable to all elements in the other,
but each set retains its own ordering.
- Figure 11 shows the linear sum of P and Q, written P⊕Q. In the linear sum, each set retains its own ordering, but additionally each maximal element of the first set is covered by each minimal element of the second set. The first set is an antichain, so all its elements are trivially maximal. The second set has three minimal elements, and an edge is drawn down from each of the three minimal elements of Q to each of the five maximal elements of P.
- Figure 12 shows the linear sum of Q and P, written Q⊕P. In the linear sum, each set retains its own ordering, but additionally each maximal element of the first set is covered by each minimal element of the second set. The first set has one maximal element (which is thus a maximum). The second set is an antichain, so all its elements are trivially minimal, and an edge is drawn down from each of the five minimal elements of P to the single maximal element of Q.
Down-sets and up-sets
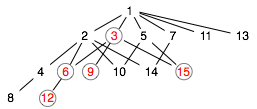
Figure 13. Down-set ↓3 of ordered set of Figure 8
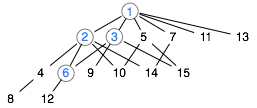
Figure 14. Up-set ↑6 of ordered set of Figure 8
A subset Q of ordered set P with order ⊑ is a down-set of P if whenever x∈Q, y∈P, and y⊑x, then y∈Q. Informally, Q contains one or more maximal elements and every member of P that is below any member of Q.
Dually, a subset Q of ordered set P with order ⊒ is an up-set of P if whenever x∈Q, y∈P, and y⊒x, then y∈Q.
Let R be an arbitrary subset of ordered set P with order ⊑. Then the smallest down-set containing R, denoted ↓R and pronounced "down R", is the set of all x∈P for which there is a y∈R such that x⊑y.
Dually, the smallest up-set containing R, denoted ↑R and pronounced "up R", is the set of all x∈P for which there is a y∈R such that x⊒y.
If R is a singleton set {r}, then we may write ↓r in place of ↓{r} or ↓R; or, dually, ↑r in place of ↑{r} or ↑R. Such down-sets (up-sets) are termed principal down-sets (up-sets) of P.
Examples, using the ordered set P shown in Figure 8:
- Q={3,6,9,12,15} is a down-set of P (Figure 13). To test this, pick any element x of Q and any element y of P; then if x|y, y∈Q. For example, pick 6 from Q. Every element that 6 divides is in Q (in this case, the element 12). The same will be true of any element you pick from Q.
- Q={3,6,9,12,15} is in fact a smallest down-set and even a principal down-set of P; it is ↓3. It appears that only in infinite ordered sets is it possible that a down-set is not also a smallest and principle down-set.
- Q={1,2,3,6} is an up-set of P (Figure 14). To test this, pick any element x of Q and any element y of P; then if y|x, y∈Q. For example, pick 6 from Q. Every element that 6 divides is in Q (in this case, the elements 1, 2, and 3). The same will be true of any element you pick from Q.
- Q={1,2,3,6} is in fact a smallest up-set and even a principal up-set of P; it is ↑6.
For further reading
B. A. Davey and H. A. Priestley. Introduction to Lattices and Order. Cambridge University Press, 2002.

