Sets
Relations
Correspondences
Ordered Sets
Lattices
Graphs
Powersets
Binary Strings
Logic
AIA
Greek
Glossary
Abstracts
Argument
Inquiry Cycle
Legal Relations
Presentations
Elicitation
Glossaries
Goals
i*
SCR
Tracing
Design Patterns
Javadoc
Java Packages
Java Types
The powerset of a set S is the set of all S's subsets.
The elements of a powerset are themselves sets, always (because each element is a subset of S).
We write the powerset of a set S as ℘(S) or P (S) or 2S (I'm going to use ℘ because it's easier to do in HTML). The ℘ is a script P (for "powerset"). You will see below why 2S is a plausible notation.
Here are some examples, using a, b, c, ... as elements:
- ℘(∅)
- { ∅ }
(the set whose only element is the empty set).
The empty set ∅ is a subset of every set, so ∅ is in every powerset. - ℘({a})
- {∅, {a} }
{a} is present because it is a subset of itself — every set is a subset of itself. Recall that the "subset" relation is actually "subset or equal to". - ℘({a, b})
- {∅, {b}, {a}, {a,b} }.
Notice that the elements of the powerset correspond to 00, 01, 10, 11 (how?). - ℘({a, b, c})
- {∅, {c}, {b}, {b,c}, {a}, {a,c}, {a,b}, {a,b,c} }.
Notice that the elements of the powerset correspond to 000, 001, 010, 011, 100, 101, 110, 111. - ℘({a, b, c, d})
- {∅, {d}, {c}, {c,d}, {b}, {b,d}, {b,c}, {b,c,d},
{a}, {a,d}, {a,c}, {a,c,d}, {a,b}, {a,b,d}, {a,b,c}, {a,b,c,d} }.
Notice that the elements of the powerset correspond to 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
A larger example is given below.
Powersets and binary integers
The elements of the powerset of a set of n elements correspond to the n-bit binary integers from 0 to (2n-1):
- the ith bit corresponds to the presence or absence of the ith element.
Thus we can enumerate the elements of a powerset by counting from 0 to (2n-1) and for each number giving the subset containing the elements corresponding to the 1 bits.
Partially ordered sets and powersets
The elements of a powerset have a natural ordering, ⊆, and any powerset and ⊆ form a It is an ordered set because the elements have an order, and a partially ordered set (rather than a totally ordered set) because not all pairs of elements are ordered. For example, look at
- ℘({a, b}) = {∅, {b}, {a}, {a,b} }
Some pairs of elements of ℘({a,b}) are ordered, such as ∅⊆{b} and {b}⊆{a,b}. But {a} and {b} are not ordered by ⊆, because neither {a}⊆{b} nor {b}⊆{a}. That means ℘({a,b}) is a partially ordered set.
Lattices and powersets
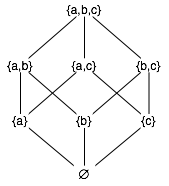
Figure 1
A diagram of the lattice for
a powerset — ℘({a,b,c})
Any powerset is also a lattice because
- it is a partially ordered set, and
- each pair of elements has a least upper bound (LUB) and a greatest lower bound (GLB).
- The LUB is the union of the two elements.
- The GLB is their intersection.
Let's talk about the LUB part.
- The union of two elements is an upper bound for them, because for any two sets S and T, S⊆S∪T.
- The union of two elements is the least upper bound for S and T because there is no set R smaller than S∪T that contains both S and T.
The same argument supports the statement that the GLB is their intersection, if you substitute "intersection" for "union" and "lower" for "upper". (This is an example of the duality of union and intersection, and of LUB and GLB.)
The powerset of {a, b, c, d, e, f, g}
Below is a larger example, a list of the elements of the powerset of {a, b, c, d, e, f, g}. The set has 7 elements so its powerset has 27 = 128 elements. This list was generated by a program.
- {∅}
- {g}
- {f}
- {f,g}
- {e}
- {e,g}
- {e,f}
- {e,f,g}
- {d}
- {d,g}
- {d,f}
- {d,f,g}
- {d,e}
- {d,e,g}
- {d,e,f}
- {d,e,f,g}
- {c}
- {c,g}
- {c,f}
- {c,f,g}
- {c,e}
- {c,e,g}
- {c,e,f}
- {c,e,f,g}
- {c,d}
- {c,d,g}
- {c,d,f}
- {c,d,f,g}
- {c,d,e}
- {c,d,e,g}
- {c,d,e,f}
- {c,d,e,f,g}
- {b}
- {b,g}
- {b,f}
- {b,f,g}
- {b,e}
- {b,e,g}
- {b,e,f}
- {b,e,f,g}
- {b,d}
- {b,d,g}
- {b,d,f}
- {b,d,f,g}
- {b,d,e}
- {b,d,e,g}
- {b,d,e,f}
- {b,d,e,f,g}
- {b,c}
- {b,c,g}
- {b,c,f}
- {b,c,f,g}
- {b,c,e}
- {b,c,e,g}
- {b,c,e,f}
- {b,c,e,f,g}
- {b,c,d}
- {b,c,d,g}
- {b,c,d,f}
- {b,c,d,f,g}
- {b,c,d,e}
- {b,c,d,e,g}
- {b,c,d,e,f}
- {b,c,d,e,f,g}
- {a}
- {a,g}
- {a,f}
- {a,f,g}
- {a,e}
- {a,e,g}
- {a,e,f}
- {a,e,f,g}
- {a,d}
- {a,d,g}
- {a,d,f}
- {a,d,f,g}
- {a,d,e}
- {a,d,e,g}
- {a,d,e,f}
- {a,d,e,f,g}
- {a,c}
- {a,c,g}
- {a,c,f}
- {a,c,f,g}
- {a,c,e}
- {a,c,e,g}
- {a,c,e,f}
- {a,c,e,f,g}
- {a,c,d}
- {a,c,d,g}
- {a,c,d,f}
- {a,c,d,f,g}
- {a,c,d,e}
- {a,c,d,e,g}
- {a,c,d,e,f}
- {a,c,d,e,f,g}
- {a,b}
- {a,b,g}
- {a,b,f}
- {a,b,f,g}
- {a,b,e}
- {a,b,e,g}
- {a,b,e,f}
- {a,b,e,f,g}
- {a,b,d}
- {a,b,d,g}
- {a,b,d,f}
- {a,b,d,f,g}
- {a,b,d,e}
- {a,b,d,e,g}
- {a,b,d,e,f}
- {a,b,d,e,f,g}
- {a,b,c}
- {a,b,c,g}
- {a,b,c,f}
- {a,b,c,f,g}
- {a,b,c,e}
- {a,b,c,e,g}
- {a,b,c,e,f}
- {a,b,c,e,f,g}
- {a,b,c,d}
- {a,b,c,d,g}
- {a,b,c,d,f}
- {a,b,c,d,f,g}
- {a,b,c,d,e}
- {a,b,c,d,e,g}
- {a,b,c,d,e,f}
- {a,b,c,d,e,f,g}

