Date: Sun, 22 Oct 2000 12:06:07 +0900 From: Toshi Kato <junk.kato@nifty.ne.jp> To: eppstein@ics.uci.edu Subject: Origamic tetrahedron
Dear David Eppstein, I made a geometical problem. Please enjoy it. Thank you, Toshi Junk Kato
Date: Sat, 21 Oct 2000 21:46:38 -0700 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
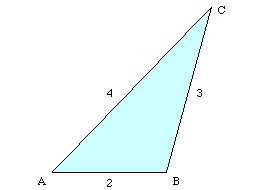
On 10/22/00 12:06 PM +0900, Toshi Kato wrote: > Here is a triangle which lengths are 2, 3 and 4. > Make a tetrahedron by folding three lines. I thought one could always fold any triangle into a tetrahedron by making four congruent triangles using folds through the midpoints of the edges. Is there something special about 2-3-4 that allows another solution? -- David Eppstein UC Irvine Dept. of Information & Computer Science eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/
Date: Sun, 22 Oct 2000 17:12:47 +0900 From: Toshi Kato <junk.kato@nifty.ne.jp> To: eppstein@ics.uci.edu Subject: Re: Origamic tetrahedron
> > Here is a triangle which lengths are 2, 3 and 4. > > Make a tetrahedron by folding three lines. > ~~~~~~~~~~~ > I thought one could always fold any triangle into a tetrahedron by making > four congruent triangles using folds through the midpoints of the edges. Is > there something special about 2-3-4 that allows another solution? Can you do it by folding only three lines about 2-3-4 triangle? Thanks for your reply. Best wishes, Junk Kato
Date: Sun, 29 Oct 2000 11:30:25 -0800 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
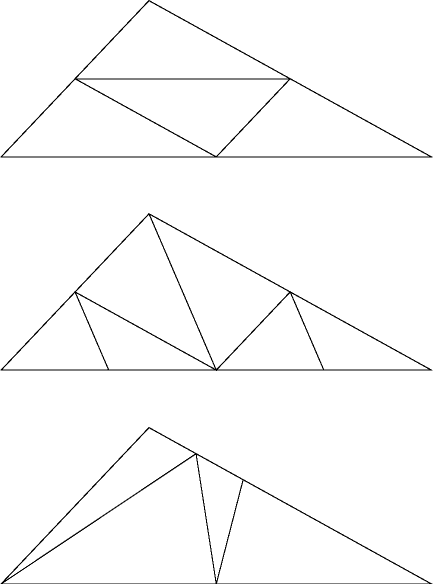
On 10/22/00 5:12 PM +0900, Toshi Kato wrote: > > I thought one could always fold any triangle into a tetrahedron by making > > four congruent triangles using folds through the midpoints of the edges. > > Is > > > there something special about 2-3-4 that allows another solution? > > Can you do it by folding only three lines about 2-3-4 triangle? You're right, this is a good puzzle. I had to actually try folding some paper in order to understand it. The four congruent triangle "solution" (top part of attached GIF image) doesn't work. It is possible to get a tetrahedron in which each of the original triangle edges is doubled back along its midpoint, but it takes more than three folds (middle of GIF). My solution is the bottom of the GIF. The fold points are at the middle of the long edge, and 1/6 and 1/3 of the way along the middle edge. -- David Eppstein UC Irvine Dept. of Information & Computer Science eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/
Date: Mon, 30 Oct 2000 11:01:55 +0900 From: Toshi Kato <junk.kato@nifty.ne.jp> To: eppstein@ics.uci.edu Subject: Re: Origamic tetrahedron
Dear Prof. David Eppstein, > You're right, this is a good puzzle. I had to actually try folding some > paper in order to understand it. > > The four congruent triangle "solution" (top part of attached GIF image) > doesn't work. It is possible to get a tetrahedron in which each of the > original triangle edges is doubled back along its midpoint, but it takes mor e > than three folds (middle of GIF). > > My solution is the bottom of the GIF. The fold points are at the middle of > the long edge, and 1/6 and 1/3 of the way along the middle edge. Very good. You are right. You are first solver. Thank you very much. If you have time, please find other solution. Best wishes, Junk Kato
Date: Sun, 29 Oct 2000 23:08:16 -0800 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
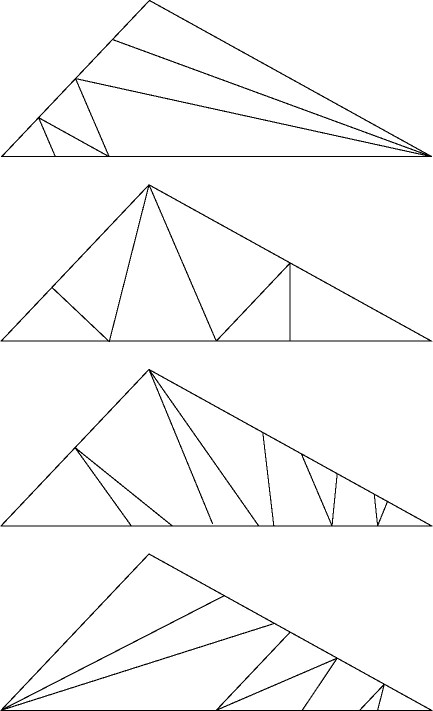
On 10/30/00 11:01 AM +0900, Toshi Kato wrote: > If you have time, please find other solution. There's more than one three-fold tetrahedron? I did try folding it some more, and found other tetrahedra, but they need five, seven, or even nine folds -- see attached image. -- David Eppstein UC Irvine Dept. of Information & Computer Science eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/
Date: Mon, 30 Oct 2000 23:54:01 +0900 From: Toshi Kato <junk.kato@nifty.ne.jp> To: eppstein@ics.uci.edu Subject: Re: Origamic tetrahedron
Dear David Eppstein, > > If you have time, please find other solution. > > There's more than one three-fold tetrahedron? Yes, I think there is one more. > I did try folding it some more, and found other tetrahedra, but they need > five, seven, or even nine folds -- see attached image. Thank you for other folds. Best wishes, Junk Kato
Date: Mon, 30 Oct 2000 12:57:38 -0800 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
On 10/30/00 11:54 PM +0900, Toshi Kato wrote: > > There's more than one three-fold tetrahedron? > > Yes, I think there is one more. Ok, I found it. It is an N-shape, with vertices one unit along the length-3 side, 1.5 units along the long side, at the obtuse vertex, and 3 units along the long side. (Image attached.) I found this by systematically going through all ways of making an N shape in the triangle, with one vertex of the N at a triangle vertex. One way gave my previous solution, four of them led to the four folds I showed you in my previous message (all with more than three folds), and the sixth led to this solution. By the way, there are also three infinite families of tetrahedra that can be folded from the triangle. if you fold two of the triangle edges in half, so that all three vertices meet at a point, you get a shape with one remaining edge (forming a continuous loop) and two interior vertices at the midpoints of the original triangle. The other two tetrahedron vertices can be chosen to be any two opposite points from the loop. There is one solution in common to all three such families: the one I first sent you. However, it seems that none of these possibilities uses only three folds. -- David Eppstein UC Irvine Dept. of Information & Computer Science eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/
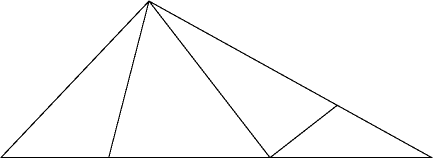
Dear Prof. Eppstein, > On 10/30/00 11:54 PM +0900, Toshi Kato wrote: > > > There's more than one three-fold tetrahedron? > > > > Yes, I think there is one more. > > Ok, I found it. It is an N-shape, with vertices one unit along the > length-3 side, 1.5 units along the long side, at the obtuse vertex, > and 3 units along the long side. I have to apologize you for my mistake. The second one is not a solution because of non-tetrahedoron. It seems that the problem has unique solution. Best regards, Junk Kato
Date: Mon, 13 Nov 2000 21:38:11 -0800 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
On 11/14/00 1:41 PM +0900, Toshi Kato wrote: > I have to apologize you for my mistake. > The second one is not a solution because of non-tetrahedoron. > It seems that the problem has unique solution. It looked like a tetrahedron when I folded it...are you sure? -- David Eppstein UC Irvine Dept. of Information & Computer Science eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/
Date: Tue, 14 Nov 2000 19:35:41 +0900 From: Toshi Kato <junk.kato@nifty.ne.jp> To: eppstein@ics.uci.edu Subject: Re: Origamic tetrahedron
Dear Prof. Eppstein, > > On 11/14/00 1:41 PM +0900, Toshi Kato wrote: > > I have to apologize you for my mistake. > > The second one is not a solution because of non-tetrahedoron. > > It seems that the problem has unique solution. > > It looked like a tetrahedron when I folded it...are you sure? I also looked like a near-flat tetrahedron at first. Now I think that it is perfect-flat. How are you feeling? Best wishes, Junk Kato
Date: Tue, 14 Nov 2000 23:26:44 -0800 From: David Eppstein <eppstein@ics.uci.edu> To: Toshi Kato <junk.kato@nifty.ne.jp> Subject: Re: Origamic tetrahedron
On 11/14/00 7:35 PM +0900, Toshi Kato wrote:
> I also looked like a near-flat tetrahedron at first.
> Now I think that it is perfect-flat.
> How are you feeling?
You are right, it is flat.
Proof:
Let the triangle be ABC, with AB=2, BC=3, AC=4.
Draw D on AC at distance 1 from A, E = midpoint(D,C), and
F on BC at distance 2 from B.
My proposed fold pattern was along line segments BD, BE, and EF.
Then BCD is isosceles, so 2*angle(BDC)+angle(BCD)=180.
But also angle(ADB)+angle(BDC)=180, so subtracting the two equations
gives angle(BDC))+angle(BCD)=angle(ADB), so these three angles
fold flat rather than making one of the corners of a tetrahedron, QED.
One can also observe that ADB is similar to ABC, BDE is isosceles,
and (since the other tetrahedron corners must also be flat) BEF is a right
triangle. I don't know of any similar nice property for the remaining
triangle, EFC. This construction also makes it clear that the sharp angle of
the 2-3-4 triangle is twice that of a 1-sqrt(15)-4 right triangle, which is
helpful if you want to calculate the angles.
--
David Eppstein UC Irvine Dept. of Information & Computer Science
eppstein@ics.uci.edu http://www.ics.uci.edu/~eppstein/