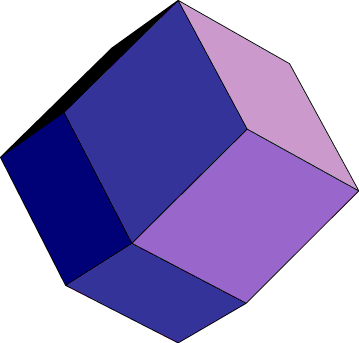
One type of decomposition I have been studying recently is hexahedral meshing: decomposing shapes into cuboids. For instance, this shape, known as the rhombic dodecahedron

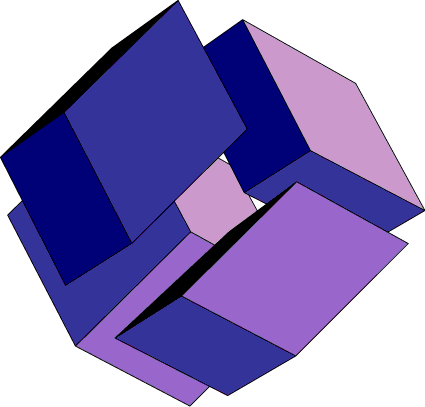
can be decomposed into four cuboids:
However, it is still open whether a similar decomposition into cuboids exists for the following octahedron:
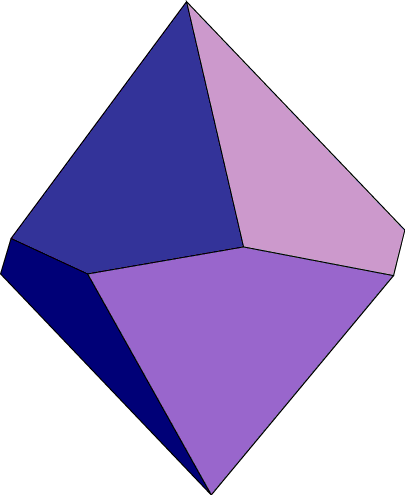
Methods from my recent paper, "Linear complexity hexahedral mesh generation", and related work by Scott Mitchell and Bill Thurston, prove that this octahedron can be meshed if we allow the cuboids to have curved sides. But it is not known whether it can be meshed by straight-sided cuboids.
More generally, we would like to know under what conditions a hexahedral mesh exists, and we would like to find algorithms that construct these meshes whenever they exist. Other research issues here include the number of cuboids needed to mesh a given shape, and the quality of the cuboid shapes.