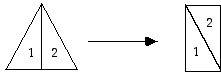
Esthetics is the study of beauty and of the criteria people use to judge what is beautiful. These criteria can be particular to a group; for instance, Romans used color schemes in villas that they found attractive–but many today find them garish and even ugly. Still, the criteria humans use to judge the beauty of some things seems to transcend time, group and culture.
In this exercise, you will determine whether certain rectangles used in Shoshoni and Crow artwork have proportions that the ancient Greeks found particularly pleasing. You will use productivity tools to analyze the data and prepare a report of your findings.
"Since early antiquity, societies have expressed esthetic preferences for rectangles having certain width (w) to length (l) ratios. Plato, for example, wrote that rectangles whose sides were in a ratio of 1 : √ 3 (about 0.577) were particularly pleasing. (These are the rectangles formed from the two halves of an equilateral triangle.)
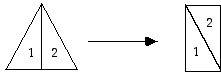
"Another ‘standard’ calls for the width to length ratio [of the rectangle] to be equal to the ratio of the length to the sum of the width and length. That is,
This implies that the width is approximately 0.618 times as long as the length.
“The Greeks called this the golden rectangle and used it often in their architecture...Other cultures also adopted this particular width to length ratio. The Egyptians built their pyramids out of stones whose faces were golden rectangles...the golden rectangle remains an architectural and artistic standard. Even items like drivers' licenses, business cards, and picture frames are often made in approximately the same proportions.” [Larsen & Stroup, 1976]
This ratio between width and length in a golden rectangle–about 0.618–is known as the Golden Ratio.
1) Determine if beaded rectangles used by Shoshoni artists to decorate their leather goods are golden rectangles.
2) Determine if rectangles used in Crow artwork are golden rectangles.
3) Determine if the Crow and Shoshoni rectangles follow Plato's standard.
Table 1 shows the width-to-length ratios (times 100) of twenty representative Shoshoni rectangles; Table 2 shows the ratios (times 100) of ten representative Crow rectangles:
Table 1 - Shoshoni width-to-length ratios (x 100)
| 69.3 | 65.4 |
| 66.2 | 61.5 |
| 69.0 | 66.8 |
| 60.6 | 60.1 |
| 57.0 | 57.6 |
| 74.9 | 67.0 |
| 67.2 | 60.6 |
| 62.8 | 61.1 |
| 60.9 | 55.3 |
| 84.4 | 93.3 |
Table 2 - Crow width-to-length ratios (x 100)
| 58.7 | 58.8 |
| 85.0 | 86.2 |
| 52.2 | 44.7 |
| 66.6 | 57.1 |
| 52.9 | 48.3 |
• Place these two tables into an Excel spreadsheet. Think carefully about the best way to organize the data so you can easily and accurately complete the steps below (a representational issue), and so the data are easy for another to read and understand (a presentational issue). For instance, do you want to place these tables onto the same sheet, or separate ones?
Using graphs
• Chart the Shoshoni values from smallest to largest (when read left to right across the page). There are a couple of ways to make a chart in Excel. Perhaps the easiest way is to select the data you wish to chart and then click on the Chart Wizard button in the toolbar across the top of the screen (it’s typically right under Help and looks like a small barchart). ChartWizard will appear; follow its instructions. Choose the type of chart, and the charting options, that allows the clearest presentation of the data; you should experiment by trying several types of charts with several option settings before making a decision on one. Include enough labeling information so a reader is quite clear about what is being shown.
• Make another chart of the Crow data, also ordered smallest to largest.
• On each chart, have a line at 61.8, the Golden Ratio times 100. Also have a line at 57.7, Plato's preferred ratio (times 100). Perhaps the easiest way to do this is to have a column of 20 cells of 61.8 and another column of 20 cells of 57.7 for the Shoshoni data; three columns in all. Then, graph all three sets of data on the same graph. Do the same for the Crow data. The Chart Wizard has easy-to-useoptions for making very readable graphs of multiple data sets. Remeber your goal to be make the chart as clear and clean as possible: in particular, more (clors, lines, marks, etc.) is not always better!
• Do these charts support the view that Shoshoni and Crow used golden rectangles? Do they support the view that they used “Plato rectangles?” We should point out that looking at graphs of these measurements only gives you a rough idea of “what's going on.” Statistical tests (such as the one used below) are much more reliable measures.
Using an appropriate statistic
A better way than “eyeballing” the data is to use statistical measures to determine if relationships hold. One good way to look at this data is to see if the arithmetic mean (the average) of the Shoshoni and Crow ratios are the same as the Golden Ratio or Plato’s standard. If there is a standard in effect then, on average, we would expect it to be followed; we would expect the average of the artworks to be the same as the Golden Ratio if that standard were being followed, or the same as Plato’s ratio, if that standard were being used. For simplicity in the discussion that follows, we'll talk about Shoshoni rectangles and the Golden Ratio; the same comments apply to Crow rectangles and to comparing either set of rectangles to Plato’s ratio.
Suppose we could measure all Shoshoni rectangular art and compute its average width-to-length ratio; that number is known as the population mean. If this mean were the same as the Golden Ratio, we would know without a doubt that the Shoshoni used that standard. If the mean were different from the Golden Ratio, we would know for certain the Shoshoni used a different standard.
But we can’t measure all Shoshoni rectangular art; the best we can do is get some of it, a sample. So instead of a population mean, we have a sample mean.
Suppose we compute a sample mean that comes out to 60.0. The population mean might actually be 61.8, the same as the Golden Ratio–the 1.8 difference could exist just because of the way we picked the items in the sample. It could also be the population mean is exactly 60.0–not the Golden ratio–because we happened to pick a sample that perfectly reflected the population. We might get another value. The problem comes to this: Given a sample mean, how do we figure out the (unknown) population mean? Once we have the population mean, we can quickly see if it is the same as the Golden Ratio.
Unfortunately, there is no way to get the population mean exactly when we only have a (small) sample; the best that can be done is to use a statistical approach:
1) Make an assumption, a statement of belief–a hypothesis–about the situation. Given the information we have, it’s quite reasonable to suspect that the Shoshoni used the Golden Ratio in their rectangular artwork. So our hypothesis is “the population mean of the Shoshoni rectangles is equal to the Golden Ratio.” Now we try to show that our assumption is false. If we show the hypothesis cannot be false, then it follows it must be true.
This seemingly torturous approach is required because you cannot prove (say with certainty that) a hypothesis is true. If our hypothesis was that the Golden and Shoshoni ratios were the same, and we got a result that showed the two ratios were indeed the same, all that tells us is that the population mean might be the same as the Golden Ratio. It could be that we just happened to choose a sample whose average matched the Golden Ratio; had we chosen a different sample, the average might well have been different. But if we can show with certainty that the Golden ratio and the sample mean cannot be different (within a chosen tolerance for sampling error, as discussed below) then they are the same because the really are the same, not just because of the way the sample was chosen.
2) Showing our assumption is false means proving that there is a real difference between the sample and population means, that they are not different just due to chance. We thus need to figure out if any difference between M (assumed to be equal to the Golden Ratio) and the sample mean m is because of chance or because they are truly distinct. If the difference is large enough, we can say the means are distinct; if not large enough, then we can’t say for sure one way or the other. Another way to say this is that if the difference of means is greater than a limit (call it z), we consider the averages to be distinct; if not, we consider our hypothesis unproved. Expressed yet another way:
if |M—m| > z is true, M and m are truly (statistically) different
3) But how do we determine a z that makes sense? Fortunately, statisticians have worked out a way to answer this question. First we normalize the difference of the means; this procedure allows us to use some standard values (often looked up in tables) for our limit. We normalize the difference by dividing it by
where n is the number of items in the sample, and s is the standard deviation of the sample.
This normalization changes our reasoning to:
if |M—m|/(s/√n) > t is true, the means are different
where t is the standardized limit.
This test is known as a t-test, after the t used in the above formula.
4) Now we need to find a value for t. Many values of t exist; the value we use depends on the sample size and on how confident we want to be if we say that M and m are different. For instance, we could say we want at least a 99% chance that we are right when we say “The Shoshoni did not used the Golden Ratio in their rectangular artwork.” Once that decision is made, we can determine t from published tables. Here are some t values for different chances in being right when we say the means are different, for our two sample sizes:
| Chance of being right when we say means are different | Sample Size of 20 | Sample Size of 10 |
| 99.95% | 3.883 | 4.781 |
| 99.50 | 2.861 | 3.250 |
| 98.00 | 2.539 | 2.821 |
| 97.50 | 2.093 | 2.262 |
| 95.00 | 1.729 | 1.833 |
| 90.00 | 1.328 | 1.383 |
| 75.00 | 0.688 | 0.703 |
| 60.00 | 0.257 | 0.261 |
So we figure out the normalized difference and compare it to our chosen t value to decide whether the Shoshoni used the Golden ratio as a standard for their rectangles in art. An example: Suppose we discover the normalized mean is 1.35. Further suppose we want at least a 90% chance of being right when we say the means are different–so we would choose a t value of 1.328. Since the normalized mean (1.35) is greater than our limit (1.328), we would conclude the Shoshoni average is indeed different from the Golden ratio.
Choosing t is critical to our conclusion. Suppose we wanted to be extremely sure that the means were different before we considered them (statistically) distinct. Let’s say we wanted to be sure that 1999 times out of 2000 (99.95%) that the means were different. Since 1.35 is less than 3.883, the t value at 99.95%, we would conclude that the means are not statistically different! Choosing a t value is, in effect, expressing how sure you want to be that the means are distinct before you commit yourself to saying they are distinct–different people have different “tolerances” for being wrong. Most statisticians don’t feel comfortable that a result is “real” unless the confidence in it exceeds 95% or even 99%.
• Compute the averages and standard deviations of the Shoshoni and Crow samples. [Hint: Excel has built-in functions that make this step quite easy.]
• Compute the normalized differences of the Crow and Shoshoni means from the Golden Ratio. (Remember, we are treating the Golden Ratio as the hypothetical population mean M.) Do the same for Plato’s ratio used as the population mean.
• Compare these normalized differences with the t values in the table above. What do you conclude from the t-test results?
Using logical reasoning and contextual information:
In addition to the charts and t-test results, you can (and should!) use logical inference based on those results and other relevant information when coming to your conclusions about whether the Shoshoni used the Golden Ratio.
For instance, suppose your t-test failed to show that the Shoshoni artworks’ ratio was different from the Golden Ratio. From this alone, you can only conclude that you cannot disprove your hypothesis. It might be the difference between the Golden ratio and the sample mean is only due to the way the sample was chosen, and the means really are the same. But, it might also be the difference is real, but too small to allow you to say so with confidence. Yet, we’re talking about comparing averages. If the average of your sample is not significantly different from the Golden ratio, then it must either be equal or very close to it–so you could say that it is very likely that the Shoshoni used the Golden ratio in their rectangular art.
But how could you be even more certain of you conclusions? Use more data and further reasoning. Suppose you decided to research the history of the Greek and Shoshoni peoples to see if their two cultures ever had contact (before modern times). Suppose you located a trusted historical source which showed that, early in their history, the Shoshoni were visited by a Greek exploratory force that included a philosopher who noted that the Shoshoni’s use of the Golden Ratio was similar to the Greek’s. Well, your case that the Shoshoni used the Golden Ratio in their art just got much, much stronger!
• Use all the information presented in this exercise (except the example in the previous paragraph–I made it up!) and all the logic you can muster in coming to your conclusion. Reason well and carefully.
Task 3 - Writing the report:
Now that you have collected and analyzed the data, and thought much about what it all means, it is time to write your report; follow the guidelines given above (under “What to turn in”). Your report will not be graded on what you decided about the Crow or Shoshoni artwork vis-a-vis the ratios, but on how well you have supported your opinion–the correctness, completeness and clarity of your reasoning. Grading will also take into account your report’s organization, how easy the report is to read and understand, the degree to which you have avoided spelling and grammatical errors and–in keeping with a main theme of this course–how well, in general, you have presented your information.
For potential extra credit
• Expand your report to include other statistics, graphics, etc. that help to support your conclusions.
• Research the Shoshoni and Crow cultures (using the Web, books, articles, people’s memories, etc.) and include information from those sources that bolsters your reasoning and conclusions. Don’t forget to reference your sources.
Remember, just adding information to the report will not earn you extra credit; the information must be relevant to the question at hand and integrated into your report and your conclusions must take the additional information into account.
1. Larsen, Richard J., and Donna Fox Stroup, Statistics in the Real World, A book of Examples, Macmillan, 1976, pp. 41-52.
2. Freund, John E, Modern Elementary Statistics, 5th edition, Prentice-Hall, 1979, pp. 247-254, 259-278.
Written by Norman Jacobson, June, 1993. Inspired by the example “Experimental esthetics,” from Larsen and Stroup, and similar exercises used in ICS21
Revised for ICS 80N Summer 1994 by Norman Jacobson, June 1994
Revised for ICS 1A, Social Science section, by Norman Jacobson, Winter 1995
Revised for ICS 80N Summer 1995 by Norman Jacobson, April 1995
Revised by Norman Jacobson, June 1997
Minor revisions for ICS 80N Summer 1998 by Norman Jacobson, June 1998
Minor revisions for ICS 1A by Norman Jacobson, September 1998
Revised for ICS 10A by Norman Jacobson, December 2000
Minor revisions to convert to a page Web page and to reflect use of Microsoft Office XP by Norman Jacobson, December 2004