
UC Irvine • Information & Computer Science • David G. Kay • Informatics 42 • Winter 2008
Review Questions for the Final Exam
These questions are representative of actual exam questions; most of them have appeared on exams in the past. But this isn't actually a sample exam, since the number and distribution of questions doesn't match an actual exam. This document includes more than one question of the same type (so you have extra practice for some of the harder concepts). Also, of course, the actual exam may cover any topic from the course, even if it's not represented here; some questions about the simulator program are possible, for example. The overall form of the exam will look more or less like last quarter's final (or the quizzes, though of course longer).
1. We can find analogies to the classic data structures in the literary world:
(a) Some large dictionaries and encyclopedias have thumb tabs for each letter, cut-outs in the edge of the volume so the reader can turn directly to the first page of listings for that letter. Is this access to the beginning of each letter's listings more like a stack, queue, array, tree, or linked list?
(b) When cookbooks describe complicated recipes, they break them into sub-recipes, much like procedures in a programming language. Thus, the recipe for a cake might say, "Use the chocolate icing recipe on page 23," and that chocolate icing recipe might say in turn, "See page 195 for instructions on melting chocolate." Which data structure would you use to represent the sequence of recipes and sub-recipes being carried out at a given moment, to make it most convenient to return to the "calling" recipe when each sub-recipe is completed: a stack, queue, array, tree, or linked list?
(c) Is a book's table of contents, with chapters, sections, and sub-sections, more like a stack, queue, array, tree, or linked list?
(d) Most newspapers run a new crossword puzzle every day. Below the puzzle it generally says, "Solution in tomorrow's newspaper." Is this sequence of puzzles and solutions more like a stack, queue, array, tree, or linked list?
(e) Some people are very rigid about reading newspapers in chronological order; they won't read one day's newspaper unless they've read all the previous days' papers, in order. Even if days or weeks go by when they don't have time to read the paper, they'll save the papers, in order, and read them in order when time permits. Is this arrangement more like a stack, queue, array, tree, or linked list?
2. At right
is a binary tree. In what order would its nodes be visited in a 
(a) preorder traversal?
(b) postorder traversal?
(c) inorder traversal?
3. Draw the binary search tree that results from inserting these items in this order: 31, 41, 59, 26, 53, 58, 62
4. Consider the following function:
int DoSomething (int a, int b)
// precondition: assume b >= 0
{ if ( b == 0 )
return (a);
else
return (DoSomething(a-1, b-1));
}
(a) What is returned by each of the following statements?
DoSomething(3, 1)
DoSomething(6, 2)
DoSomething(29, 5)
DoSomething(25000, 23000)
(b) In one English word (or in mathematical notation), describe the value this function returns in terms of its arguments.
(c) Give the recurrence relation that corresponds to the code shown above, counting each arithmetic operations (addition, subtraction, multiplication, and division):
D0 =
Dn =
(d) Now look at this function:
int DoSomethingElse (int a, int b)
// precondition: assume b >= 0
{ if ( b == 0 )
return (a);
else
return (DoSomethingElse(a, b-1) - 1);
}
(d.1) Does DoSomethingElse produce the same results as DoSomething? If not, explain how the results differ.
(d.2) Which of these routines are tail recursive--DoSomething, DoSomethingElse, neither, or both? For any non-tail-recursive routine, indicate which specific operation in its code makes it non-tail-recursive.
5. Below is the state transition diagram for an FSA. This machine reads a whole word at a time (rather than a character at a time, as we did in class).

(a) For each of the following strings, circle ACCEPT if the FSA above accepts the string and REJECT if it does not:
ACCEPT REJECT
Jill eats tantrums
ACCEPT REJECT Joe eats loud
big bad big big apples
ACCEPT REJECT Joe throws apples
ACCEPT REJECT Jill eats
ACCEPT REJECT Joe throws loud
loud tantrums
ACCEPT REJECT Jill throws Joe
(b) Draw a transition table for the FSA shown above. You may leave transitions to the error state blank rather than writing in "ERROR."
Jill Joe throws eats big bad loud tantrums apples OTHER
S1_______________________________________________________________________
S2_______________________________________________________________________
S3_______________________________________________________________________
S4_______________________________________________________________________
(c) Modify the FSA diagram above so that Jane may also occur anywhere Joe or Jill may occur (in the language accepted by the FSA).
(d) Draw a new FSA that accepts the language containing the following six sentences (and no others):
Joe likes plums Joe likes big plums
Joe likes very big plums
Joe eats plums Joe eats big plums Joe
eats very big plums
6. Below is the state transition diagram for an FSA.

(a) Give three examples of strings that the machine described above accepts.
(b) Give three examples of strings (using the same alphabet) that the machine described above rejects.
(c) In one brief English sentence, describe the language that this machine implements.
(d) Describe this language using a regular expression--that is, using just the input symbols, parentheses, the union symbol, and asterisks.
(e) Modify the FSA diagram above so that it accepts
the language a*(b![]() c)a*
(that is, any string of zero or more 'a's,
followed by a b
or a c,
followed by zero or more 'a's).
You may draw your answer on the printed diagram.
c)a*
(that is, any string of zero or more 'a's,
followed by a b
or a c,
followed by zero or more 'a's).
You may draw your answer on the printed diagram.
(f) Draw a state transition table below that reflects the new machine described above in part (e).
7. One way to represent transitions in a finite-state machine is in a transition table; the entries in the table show the machine's next state, given its current state and a particular input. The table at left below implements the machine shown at right below.
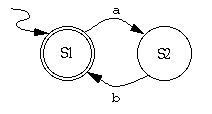
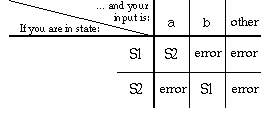
(a) Give four examples of strings that the machine described above accepts.
(b) Give four examples of strings (using the same alphabet) that the machine described above rejects.
(c) In one brief English sentence, describe the language that this machine implements.
(d) Describe this language using a regular expression--that is, using just the input symbols, parentheses, the union symbol, and asterisks.
(e) Modify the FSA diagram above so that it accepts the language (a*bc)* (that is, any string of zero or more parts, where each part contains any number of 'a's followed by a 'b' and a 'c').
(f) Modify the transition table above to reflect the new machine described in part (e).
8. Below is a finite-state machine that accepts telephone numbers ('digit' means any decimal digit, 0-9):
http://www.ics.uci.edu/~kay/courses/i42/phonenumber.jpg
(a) Draw the state transition table for this FSA.
You may leave blank any unspecified transitions; you may omit the error
state. We have supplied horizontal lines; you will supply the vertical
lines and everything else. (Hint: Don't treat all digits the same.)
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
(b) Following the approach shown in class, which of the statements shown below could be part of a program to implement an FSA with a transition table? Circle the one best answer.
A. Table[state][token]
= state;
B. state
= (Table[state][token])++;
C. Table[state][token]
= Table[state++][token];
D. (Table[state][token])++;
E. state
= Table[state][token];
F. token
= Table[state][token];
Below is a BNF grammar that also describes telephone
numbers:
<phone number>
::= <local number> | <area
code> <local number>
<area code> ::= 1
( <digit> <digit>
<digit> )
<local number>
::= <exchange> <hyphen> <number>
<exchange> ::= <digit> <digit>
<digit>
<hyphen> ::= -
<number>
::= <digit> <digit> <digit> <digit>
<digit> ::= 0
| 1 | 2 | 3 | 4 | 5 | 6 | 7
| 8 | 9
(c) Unfortunately, the BNF grammar and the FSA (reproduced again below for convenience) do not both specify the same "language." For each string listed below,
* circle VALID IN BNF or INVALID IN BNF to indicate which strings can be generated from <phone number> in the grammar given above, and
* circle ACCEPTED BY FSA or REJECTED BY FSA to indicate which strings would be accepted by the FSA.
VALID IN BNF INVALID IN BNF 824-5072 ACCEPTED BY FSA REJECTED BY FSA
VALID IN BNF INVALID IN BNF 123-4567 ACCEPTED BY FSA REJECTED BY FSA
VALID IN BNF INVALID IN BNF 411 ACCEPTED BY FSA REJECTED BY FSA
VALID IN BNF INVALID IN BNF 2-9-7689 ACCEPTED BY FSA REJECTED BY FSA
VALID IN BNF INVALID IN BNF (310)825-2695 ACCEPTED BY FSA REJECTED BY FSA
VALID IN BNF INVALID IN BNF 1(000)000-0000 ACCEPTED BY FSA REJECTED BY FSA
http://www.ics.uci.edu/~kay/courses/i42/phonenumber.jpg
(d) Modify the FSA (by drawing on the diagram above) so that it accepts exactly the same phone numbers as the BNF grammar accepts.
9. Suppose you have a conventional stack with operations push, pop, and top.
(a) What is printed by the following sequence of operations?
push(5); push(4); print(top()); push(7); push(12); pop; print(top()); print(top()); pop();
(b) What are the contents of the stack at the end of the sequence of operations? Mark clearly the top and bottom of the stack.
10. Give the recurrence relation that describes the execution time of the second routine shown below, the Print member function of the Collection class, counting println statements. Just give the recurrence; you don't have to solve it.
void Print() // member function of restaurant
{
System.out.println("Name: " + name);
System.out.println("Cuisine: " + cuisine);
System.out.println("Phone: " + phone);
System.out.println("Best dish: " + dish);
System.out.println("Price: " + price);
}
void Print() // method0 of a restaurant _collection_
{
if (IsEmpty()) // if this collection is empty,
System.out.println();// print a newline.
else
{ // else print the first restaurant
First().Print(); // in the collection
Rest().Print(); // and then print the rest of the
} // collection (recursively)
}
11. For each of the following code segments, give the average-case run-time polynomial and the O-notation. Count each line that contains an assignment statement (except those controlling for-loops), a procedure call, or an input/output statement.
System.out.println("This line is executed only once.");
total = 0;
for ( i = 1; i <= n; i++ ) {
int x = readAnInteger(); // count this line once
total += x;
if ( i % 2 == 0 )
System.out.println(x);
}
System.out.print("Total: ");
System.out.println(total);
System.out.println("The end.");
Example answer: Runtime polynomial: 2 + n (2 + 1/2) + 3, which is 2.5n + 5; O(n).
(a)
for ( i = 1; i < n; i++ )
for ( j = n; j >= 1; j-- )
for ( k = 1; k <= n/2; k++ )
Data[i,j,k] = i + j + k;
System.out.println("On the whole, I'd rather be in Philadelphia.");
(b)
System.out.print("With more powerful tools ");
System.out.print("comes the power to screw up ");
System.out.println("in new and more spectacular ways.");
int a = 1;
while (a <= n)
{
DanceAJig( a );
for ( i = 1; i <= n; i++ )
{ if ( i % 2 == 0)
{
DanceAReel( a, i );
DanceAPasDeDeux( a*i );
}
System.out.println("Swing your partner to and fro");
}
a++; // This counts as an assignment.
}
System.out.println("People time is more expensive than computer time.");
(c)
System.out.println("Now, the Star-Belly Sneetches had bellies with stars.");
System.out.println("The Plain-Belly Sneetches had none upon thars.");
int a = 1;
while (a <= n)
{
DoSomethingGood(a);
for ( i = n; i >= 1; i-- )
{ DoSomethingBad(a, i);
HandleSomethingElse( a*i );
}
for ( i = 1; i <= 64000; i += 2 )
{ DoSomethingBad(a, i);
HandleSomethingElse( a*i );
}
a *= 2;
}
System.out.println("Those stars weren't so big. They were really so small ");
System.out.println("You might think such a thing wouldn't matter at all.");
(d) Suppose that all three of the above program segments were included in one function. What would the O-notation of that function be?
12. (a)  One way to implement a priority queue is in
a binary search tree ordered by priority value, where each node of the tree
(representing a distinct priority value) stores all the items with the same
priority, in a linked list ordered by "arrival time." Shown is
a diagram of this approach, after the following [priority, item] pairs have
been enqueued: [5,A] [8,B] [5,D] [2,E] [7,F] [7, G].
On the diagram above, draw the results
of enqueueing these items: [8,K] [2,M] [3,P]
One way to implement a priority queue is in
a binary search tree ordered by priority value, where each node of the tree
(representing a distinct priority value) stores all the items with the same
priority, in a linked list ordered by "arrival time." Shown is
a diagram of this approach, after the following [priority, item] pairs have
been enqueued: [5,A] [8,B] [5,D] [2,E] [7,F] [7, G].
On the diagram above, draw the results
of enqueueing these items: [8,K] [2,M] [3,P]
(b.1) You are designing some web server software that will handle thousands of requests for information from your web site. You decide that those requests should be prioritized-- perhaps system troubleshooting receives top priority, full-rate-paying customers receive next priority, discount customers receive lower priority, and guests receive the lowest.
You decide to use a priority queue for these requests, and you consider three different data structures for implementing it:
Structure I: An unordered array where each element contains a priority, the time the request arrived, and the other information about a request; you also have an additional field that contains the number of requests currently stored.
Structure II: A binary search tree as described above. (You may assume that priority nodes never get deleted--they just may have empty item lists after all items with that priority are dequeued.)
Structure III: A linear linked list, completely ordered (by priority, and for equal priorities by arrival time) so that the correct item to dequeue is always at the front.
In the table below, fill in the O-notation for the execution time of each specified operation on each alternative data structure in the average case. Assume that on average there are r requests in the whole data structure, i different items that have each different priority value, and p different priority values; use whichever of these variables are appropriate in your answers. Also assume that each operation is implemented as efficiently as possible in Java (without adding unspecified variables or otherwise changing the structure described).
| Operations: | Structure I | Structure II |
Structure III |
| Front (number of comparisons) |
|
||
| Enqueue (number of comparisons) |
|
||
| Enqueue (number of data movements) |
|
||
| Dequeue (number of comparisons) |
|
||
| Dequeue (number of data movements) |
|
||
| SizeOf (number of comparisons) |
|
| Storage required |
|
(c.2) If your priority queue gets very large, which structure provides the fastest dequeueing?
(c.3) If your priority queue gets very large, which structure provides the best overall performance on enqueueing and dequeueing?
(d) Give the most convincing real-world example you can (not necessarily web server software) for implementing a priority queue that ...
(d.1) enqueues as quickly as possible (with other operations' performance less important), as in (c.1)
(d.2) dequeues as quickly as possible (with other operations' performance less important), as in (c.2)
(d.3) has even performance for enqueueing and dequeueing
13. Suppose you have a conventional queue with operations enqueue, dequeue, and front.
(a) What does the following sequence of operations print:
enqueue(3); enqueue(7); enqueue(5); print(front()); dequeue(); print(front()); enqueue(9);
(b) What are the contents of the queue at the end of this sequence of operations? Indicate clearly the front and the end of the queue.
14. Suppose you have a priority queue with operations enqueue, dequeue, and front. The priority of each item is its value; the first item to be dequeued is the item with the greatest numerical value.
(a) What does the following sequence of operations print:
enqueue(3); enqueue(7); enqueue(5); print(front()); dequeue(); print(front()); enqueue(9);
(b) What are the contents of the queue at the end of this sequence of operations? Indicate clearly the front and the end of the queue.
15. Suppose that you need to implement a "collection" of at least 50,000 items, with various operations. Suppose further that you are considering four alternative data structures, whose performance on each operation is shown in the table below (where n is the number of items currently in the collection).
| Operation: | Structure I | Structure II | Structure III |
Structure IV |
| Add a new item | O(n) | O (1) | O(log n) |
O(n) |
| Search for an item | O(log n) | O(n) | O(log n) |
O(n) |
| Delete an item (assuming you already know its location) | O(n) | O (1) | O(log n) |
O(n) |
| Print all the items (in any order) | O(n) | O(n) | O(n) |
O(n) |
| Print all the items (in a particular order) | O(n) | O(n log n) | O(n) |
O(n log n) |
(b.1) Suppose that you are storing the telephone directory used by directory assistance operators, where each item contains someone's name, address, and telephone number. Which of the operations listed above would you expect to be the most frequent on this collection of data?
(b.2) Which structure (I, II, III, or IV) should you choose to implement the telephone directory (and, in just a few words, why)?
(c) To delete an item in practice requires both locating the item and actually removing it (if it occurs in the collection). Which structure (I, II, III, or IV) is the most efficient for this entire process of deleting an item?
(d) Which structure(s), if any, should never be used based on the above performance measures?
(e) Give the best brief description you can of each of the structures (I, II, III, and IV) listed above. You can describe each in just a couple of words (including "tree," "queue," "stack," "linked list," or "array"), but be sure to indicate whether or not the items are stored in order, and whether or not any additional data fields, such as trailing pointers or the number of items, are required. You may include a clear picture if you like.
Structure I is a
Structure II is a
Structure III is a
Structure IV is a
16. The Department of Motor Vehicles stores registration information (including license number, owner's name, and vehicle description) on millions of vehicles. As a practical matter, the DMV can't store all the information on every vehicle in main memory (RAM); main memory will contain just an index, containing perhaps the license number or the owner's name (the "key"), together with a pointer to the bulk of the information that remains on disk. If an item's key is found in the index, the rest of its information can be retrieved with one access to the disk.
The DMV is considering four different structures for organizing the index; you may assume that the disk-based information can be traversed in linear time if necessary.
Structure I: The index is an unordered array with an additional field that contains the number of vehicles currently stored.
Structure II: The index is an array sorted by license number, with an additional field containing the number of vehicles currently stored.
Structure III: The index is a binary search tree ordered by license number.
Structure IV: The index consists of two binary search trees, one ordered by license number and one ordered by owner's name.
(a) In the table below, fill in the O-notation for each alternative data structure on each specified operation. Assume there are v vehicles in the database and that each operation is implemented as efficiently as possible in Java.
| Operations: | Structure I | Structure II | Structure III |
Structure IV |
| Add a new vehicle (number of comparisons) |
|
|||
| Add a new vehicle (number of data movements) |
|
|||
| Search for an item, given license number |
|
|||
| Search for an item, given owner's name |
|
|||
| Print all the items (in any order) |
|
|||
| Print all the items (in order by owner's name) |
|
(b) In the table below, give the O-notation for the storage (main memory) required by each structure, assuming that there are v vehicles in the database and a maximum of m vehicles possible and that each structure is designed as efficiently as possible in Pascal.
| Structure I | Structure II | Structure III |
Structure IV |
|
| Main memory required |
|
17. You want to purchase a database management program. You're considering three different products: FuzzyBase, OnBase, and HomeBase. You read a magazine article that reviews these products, which includes two graphs of their performance (on a "benchmark" task designed to be representative of typical database tasks).
The first graph shows the programs' performance on three relatively small sets of data. The second graph (on the following page) shows their performance on the same task, but with three relatively large sets of data.
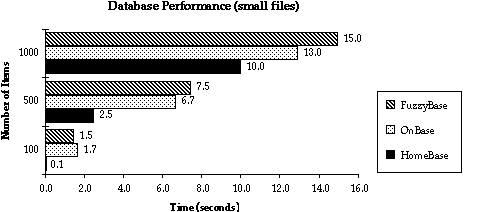
(a) Looking only at the small-files graph above, which program was the fastest in all the tests shown?
(b) Which program was the slowest in most of the tests shown on the graph above?
(c) The 1000-item test is 10 times larger than the 100-item test. How many times longer does FuzzyBase take to do the 1000-item test than the 100-item test?
(d) How many times longer does HomeBase take to do the 1000-item test than the 100-item test?
(e) From the data shown above, what is the likeliest O-notation for the execution time of FuzzyBase on these benchmark tests?
(f) From the data shown above, what is the likeliest O-notation for the execution time of HomeBase on these benchmark tests?
(g) Does the fastest program in the above tests have the best O-notation? If so, explain how you can estimate the execution time from the O-notation. If not, explain how a program with worse O-notation can be faster in these tests than one with better O-notation. Answer in just one English sentence, and don't take up more space than is left on this page.
Now consider the graph of the large-file benchmarks
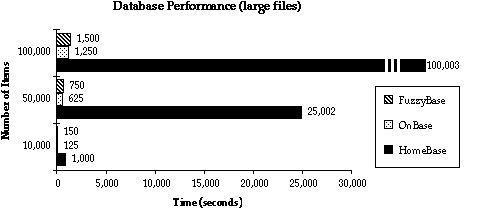
(h) Which program was the slowest in all the tests shown on the large-files graph above?
(i) Which program was the fastest in all the tests shown on the large-files graph above?
(j) Below are five alternatives; each alternative gives a polynomial expression that describes the execution time of each program on the benchmark tests. Only one alternative is consistent with all the data shown above; which alternative is the potentially correct set of expressions?
FuzzyBase OnBase HomeBase
A. 1500n + 500 n2 + 10 n2 + 3n + 23
B. n2 + 3n + 23 1500n + 50,000 750n + 45,000
C. 1500n + 500 750n + 45,000 n2 + 3n + 23
D. 1500n + 50,000 750n + 400 n2 + 3n + 23
E. 750n + 400 n2 + 3n + 23 1500n + 500
(k) In one brief English sentence, explain why the fastest program in the small-file tests was the slowest program in the large-file tests.
18. Other topics to be familiar with (that might show up, in most cases briefly, on the exam):