| Reaction | Description or Expansion |
|
|
Creation (introduction) |
|
|
Annihilation (removal) |
|
|
Standard mass action with stoichiometry |
|
|
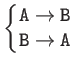 |
|
|
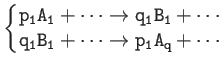 |
| Representation of
|
|
|
|
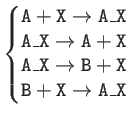 |
| Representation of
|
|
|
|
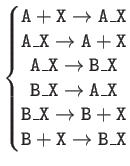 |
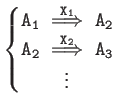
| Typical Cascades | |
|
|
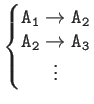 |
|
|
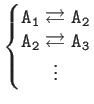 |
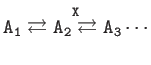 |
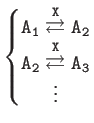 |
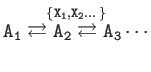 |
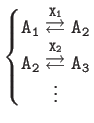 |
| Reaction | Description or Expansion |
|
|
Creation (introduction) |
|
|
Annihilation (removal) |
|
|
Standard mass action with stoichiometry |
|
|
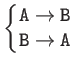 |
|
|
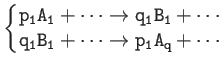 |
| Representation of
|
|
|
|
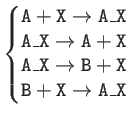 |
| Representation of
|
|
|
|
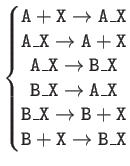 |
| Typical Cascades | |
|
|
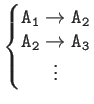 |
|
|
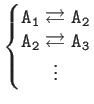 |
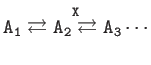 |
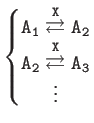 |
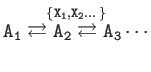 |
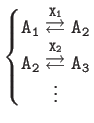 |
Syntax
![$ {\tt\{A\overset{X}\implies B, MM[K,v]\}}$](img24.png) |
|
|
|
![$ {\tt [B]'=\dfrac{v[A]}{K+[A]}=-[A]' }$](img26.png) |
|
|
![$ {\tt [B]'=\dfrac{v[A][X]}{K+[A]}=-[A]' }$](img28.png) |
|
|
![$ {\tt [B]'=\dfrac{v_A[A]}{K_A+[A]}-\dfrac{v_B[B]}{K_B+[B]}=-[A]' }$](img30.png) |
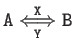 |
![$ {\tt [B]'=\dfrac{v_A[A][X]}{K_A+[A]}-\dfrac{v_B[B][Y]}{K_B+[B]}=-[A]' }$](img32.png) |
Syntax
![$ {\tt\{A\overset{X}\implies B, MM[k_1,k_2,k_3]\}}$](img34.png) |
|
|
|
![$ {\tt [B]'=\dfrac{k_1[A]}{\frac{k_2+k_3}{k_1}+[A]}=-[A]' }$](img35.png) |
|
|
![$ {\tt [B]'=\dfrac{k_1 [A][X]}{\frac{k_2+k_3}{k_1}+[A]}=-[A]' }$](img36.png) |
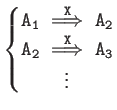
| Cascades | |
|
|
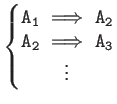 |
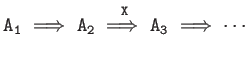 |
 |
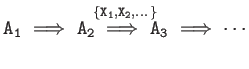 |
 |
| Syntax
|
|
|
|
![$ {\tt [B]'=\dfrac{v(b+T[A])^n}{K^n+(b+T[A])^n}}$](img45.png) and and |
| Syntax
|
|
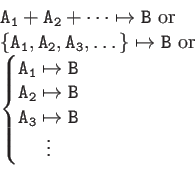 |
![\begin{displaymath}
\begin{array}{l}
{\tt [B]'=\dfrac{v(b+T_1[A_1]+T_2[A_2]+\cdo...
...2]+\cdots)^n}} \\
{\tt [A_1]'=[A_2]'=\cdots = 0}
\end{array}\end{displaymath}](img49.png)
|
Syntax
![$ {\tt
\{ A\overset{X}\mapsto B, hill[v,n,K,b,T]\}}$](img50.png) |
|
|
|
![$ {\tt [B]'=\dfrac{v[X](b+T[A])^n}{K^n+(b+T[A])^n} = -[A]' }$](img52.png) |
| Syntax
|
|
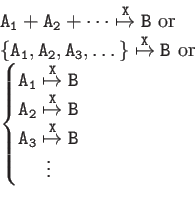 |
![\begin{displaymath}
\begin{array}{l}
{\tt [B]'=\dfrac{v[X](b+T_1[A_1]+T_2[A_2]+\...
...cdots)^n}} \\
{\tt [A_1]'=[A_2]'=\cdots = -[B]'}
\end{array}\end{displaymath}](img54.png)
|
| Syntax
|
|
|
|
![\begin{displaymath}\begin{array}{l} \\
{\tt [B]'=\dfrac{v}{1+e^{-h-\beta [A]^n}}}\\
{\tt [A]'=0 } \\
\end{array}\end{displaymath}](img57.png) |
| Syntax
|
|
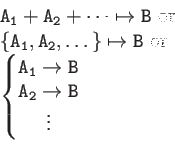 |
![\begin{displaymath}
\begin{array}{l}
{\tt [B]'=\dfrac{v}{1+e^{-h-\beta_1 [A_1]^{...
... - \cdots}}} \\
{\tt [A_1]' = [A_2]'=\cdots = 0}
\end{array}\end{displaymath}](img60.png) |
| Syntax
|
|
|
|
![$ \begin{array}{l}
\\
{\tt [B]'=\dfrac{1}{\tau}\left( K_{+}[A]^{C_{+}} - K_{-}[A]^{C_{-}} \right)}
\\
{\tt [A]'=0} \\
\end{array}$](img62.png) |
| Syntax
|
|
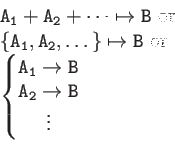
|
![\begin{displaymath}
\begin{array}{l}
{\tt [B]'=\dfrac{ K_{+}[A_1]^{p_1}[A_2]^{p_...
...2}\cdots}{\tau}} \\
{\tt [A_1]'=[A_2]'=\cdots=0}
\end{array}\end{displaymath}](img64.png) |
| Syntax
|
|
|
|
![\begin{displaymath}\begin{array}{l}
{\tt [B]'=\dfrac{v(1+\alpha [A]^n)^m}{(1+\alpha [A]^n)^m + k (1+\beta [A]^n)^m}}\\
{\tt [A]'=0}
\end{array}\end{displaymath}](img66.png) |
| Syntax
|
|
| Syntax
|
|
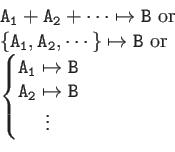 |
![\begin{displaymath}
\begin{array}{l}
{\tt
[B]'=\dfrac{v\prod_j(1+\alpha_j [A_j]^...
...{n_j})^m}
}
\\
{\tt [A_1]'=[A_2]' = \cdots = 0}
\end{array}\end{displaymath}](img70.png) |
| Syntax
|
|
| Syntax
|
|
|
|
![\begin{displaymath}\begin{array}{l}
{\tt [B]'=\dfrac{v(1+T\mathcal{U}(T)[A]^n)^m...
... + k (1+T\mathcal{U}(-T) [A]^n)^m}}\\
{\tt [A]'=0}
\end{array}\end{displaymath}](img73.png) |
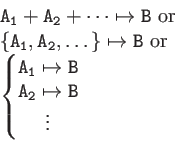 |
![\begin{displaymath}
\begin{array}{l}
{\tt [B]' =
\dfrac{v\prod_j (1+T_j\mathcal...
...]^{n_j})^m}
} \\
{\tt [A_1]'=[A_2]'=\cdots = 0}
\end{array}\end{displaymath}](img75.png) |
Syntax
![$ \{\tt A\overset{X}\Rightarrow B, MWC[k_{cat}, n, c, \ell,K]\}$](img76.png) |
|
|
|
![\begin{displaymath}\begin{array}{l}
{\tt
[B]' = k_{cat}[X]\dfrac
{\alpha(1+\alph...
... where } \alpha=\dfrac{[A]}{K}
\\
{\tt [A]'=-[B]'}
\end{array}\end{displaymath}](img78.png) |
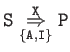 |
|
Syntax
![$ \{\tt\underset{\{\{A_1,A_2,\dots\}, \{I_1,I_2,\dots\}\}}{\{S_1,S_2,\dots\}\overset{X}\Rightarrow \{ P_1,P_2,\dots \}}, MWC[\{k_1,k_2\dots \},n,c,\ell,K]\}$](img81.png) |
|
![\begin{displaymath}\begin{array}{l}
{\tt [P_q]'=k_q[X]\dfrac
{\prod_i(1+a_i)^n ...
...ac{[A_j]}{K_{A_j}}, \
i_j = \dfrac{[I_j]}{K_{I_j}}
\end{array}\end{displaymath}](img82.png)
|
|
Syntax
![$ \{\tt\underset{
\{\{A_1,A_2,\dots\},
\{I_1,I_2,\dots\}\},
\{
\{C'_{11},C'_{12...
...overset{X}\Rightarrow \{ P_1,P_2,\dots \}}, MWC[\{k_1,k_2,\dots\},n,c,\ell,K]\}$](img83.png) |
|
|
here
|
|
![\begin{displaymath}\begin{array}{l}
[P_q]'=\dfrac
{\prod_i(1+a_i+\overline{a_...
...verline{a_j} = \sum_q\dfrac{[A'_{jq}]}{K_{A'_{jq}}}
\end{array}\end{displaymath}](img88.png) |
|
![\begin{displaymath}
\begin{array}{l}
{\tt\{\{\{ A_1, A_2,\dots \}, \{B_1,B_2,\do...
...ots\},\{b_0,\dots\},\{p_1,\dots\},\{q_1,\dots\}]\}
}\end{array}\end{displaymath}](img89.png) |
![\begin{displaymath}\begin{array}{l}
{\tt [X]'=\dfrac
{a_0 + a_1[A_1]^{p_1} + a...
...tt [A_1]'=[A_2]'=\cdots = [B_1]'=[B_2]'=\cdots = 0}
\end{array}\end{displaymath}](img90.png) |
|
|
|
|
|
|
|
|
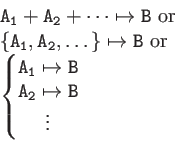 |
|
|
|
|
|
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html arrow-forms.tex -no_navigation -split 0
The translation was initiated by Snicker Snack on 2012-08-31