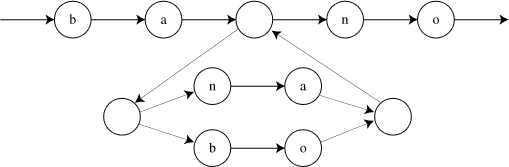
The algorithms I'm going to describe test whether some string matches a regular expression. Generally, we don't want to know that so much as whether a substring matches. We can solve this problem by introducing "wildcards", which I'll denote by a question mark. So ?*ba((na+bo)*)no?*. would match any string having a substring matching ba((na+bo)*)no.

The strings matched by the pattern then correspond exactly to the sequences of letters you go through at the vertices of paths in this graph. So we can think of the regular expression matching problem as one of finding an appropriate path in the graph, one that goes through the right vertices in the right order.
To apply dynamic programming, we'll start with a recursive algorithm for this problem, that tests for a given vertex in the graph, and a suffix of the input, whether there is a path from the start to that vertex that matches that substring.
recursive_match(graph,vertex,string,strlen)
{
for (each vertex w)
if (recursive_match(graph, w, string, strlen-1) &&
(w -> v matches string[strlen-1]))
return TRUE;
return FALSE;
}
To turn this into a dynamic program, we just remember the solutions
for each value of the vertex and strlen parameters. There are O(m)
choices of the vertex (where m denotes the length of the pattern)
and O(n) choices of strlen (where n is the length of the string to
be matched), so there are O(mn) subproblems. Each takes O(m) time
to compute (it involves a loop through each other vertex) so the
total time is O(m^2 n).
To think about how to speed this up, let's turn it into a graph path problem as before. We'll make a new big graph; think of it as being the cartesian product of the string with the smaller pattern graph we already constructed. A vertex of the new graph will correspond to pair (v,i) where v is vertex of the pattern graph and i is index into string. We add an edge (v,i) -> (w,i) if v can get to w without processing any more characters, and an edge (v,i) -> (w,i+1) if you can get from v to w while matching the single character string[i].
For instance, for the string "bano" this product graph looks like four copies of the original pattern graph. Each copy keeps only the edges that don't involve matching a character, and different copies are connected by edges that depend on the corresponding positions of the string "bano".
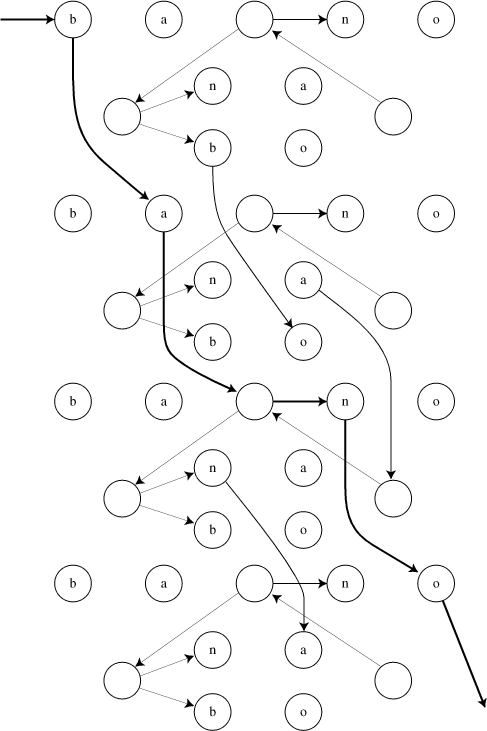
The pattern matching problem then turns out to be equivalent to reachability in this graph. Since the graph has O(mn) vertices and edges, we can test reachability and solve the regular expression matching problem in time O(mn).
Can you fit them all onto the disks?
The answer is sometimes yes, sometimes no. E.g. if the file sizes are 18x5, 1x47, 1x63 it's not possible. The two big files can't be together because they're too big, and they can't be separate because then neither side could be a multiple of ten. But 4x38, 16x3 is possible: put 2x38 and 8x3 on each side.
How to tell automatically when this problem can be solved?
As usual, let's start with a recursive algorithm. Given a sequence x1,x2,x3,...xn of positive integers and a target sum T (here n=20, T=100) then if some group of values adds to T, either xn is in the group or it isn't. So the problem is solvable if either the same sum is solvable for x1...x(n-1), or if T-xn is solvable for x1...x(n-1).
partition(X,n,T)
{
if (T=0) return true else
return (partition(X,n-1,T) or partition(X,n-1,T-X[n])
}
As often happens, this simple recursive algorithm is very
inefficient. A problem with n values leads to two subproblems with
n-1 values, so there are 2^n recursive calls. We can make some
minor improvement if we test whether T<0 and return false
immediately, but that still won't be enough to really speed up the
algorithm.
Now let's turn it into a dynamic program. As usual, we start with the memoizing version, based on the same recursion, but storing subproblem solutions. We store them in an array M[n,T] contains three values: true, false, undefined. Initially all values are assumed to be initialized to undefined.
partition(X,n,T)
{
if T<0 return false
else if T=0 return true
else if M[n,T] is undefined
M[n,T] = partition(X,n-1,T) or partition(X,n-1,T-X[n])
return M[n,T]
}
Analysis: each call takes constant time unless we fill in a new
array value. There are nT array values to fill in, each of which
involves constant time plus O(1) subroutine calls. So the total is
O(nT) time.
As usual, we can simplify this by reordering it and getting a bottom up dynamic program:
partition(X,n,T)
{
array M[n,T] of boolean values
for i = 1 to n
{
M[i,0] = true
for j = 1 to T
{
if (X[i] > j) M[i,j] = M[i-1,j]
else M[i,j] = M[i-1,j] or M[i-1,j-X[i]]
}
}
return M[n,T]
}
And as in the longest common subsequence problem, reordering saves
space and simplifies the method even further:
partition(X,n,T)
{
array M[T] of boolean
M[0] = true
for i = 1 to n
for j = X[i] to T
M[j] = M[j] or M[j-X[i]]
return M[T]
}
Like the previous two dynamic programs, this can be turned into a
graph reachability problem by making one vertex per subproblems and
connecting two vertices by an edge when one depends on the other.
Let's finish by looking at a problem, matrix multiplication, that
is different: as far as I can tell it isn't related to paths in
graphs. It's also a good example of a dynamic program in which each
recursive call is more than constant time.
Given a sequence of integers
(x1,x2,x3,...xn)
corresponding to matrices
M[x1,x2], N[x2,x3], O[x3,x4] ...
there are several ways to do the multiplication:
(M N) O or M (N O)
taking different total times:
O(x1x2x3 + x1x3x4) or O(x1x2x4 + x2x3x4)
What is the best way to multiply the matrices? how much time does
it take?
If there are only four integers in the sequence (and so only three matrices) you can just compare both possibilities, but for longer sequences there may be exponentially many different multiplication orders to test. We'd like to find the best one without testing them all.
The basic idea of the algorithm is to look at the last multiplication you do:
(M N O ... Q) (R S T ... Z)
Note that the two groups should be optimally multiplied inside
themselves. So if you only knew where to split them, you could
solve the problem using two recursive subproblems. Fortunately, it
isn't allowed to reorder the matrices, so there are only O(n)
different possible splits. We simply try them all.
It's easier to understand the solution if we instead look at list of dimensions. This is again splits into two groups,
(x1 x2 ... xk)
(xk x(k+1) ... xn)
(note that the two overlap by one integer). We want to find the
optimal value of k; we can try all possible values and choose the
one that gives the best total matrix multiplication cost.
As usual, we start with a recursive procedure.
mtime(X,i,j)
{
if (j<=i+1) return 0;
cost = +infinity;
for (k = i+1; k <= j-1; k++)
cost = min(cost, mtime(X,i,k)+mtime(X,k,j)+X[i]X[j]X[k])
return cost
}
This is inefficient (it takes exponential time). But there are only
O(n^2) subproblems being solved: that's how many ways there are of
choosing i and j. We can memoize by storing a solution T[i,j]:
array T[n,n] = {-1, -1, ..., -1};
mtime(X,i,j)
{
if (j<=i+1) return 0;
else if (T[i,j] >=0) return T[i,j];
cost = +infinity
for (k = i+1; k <= j-1; k++)
cost = min(cost, mtime(X,i,k)+mtime(X,k,j)+X[i]X[j]X[k])
T[i,j] = cost;
return cost;
}
Each call takes constant time unless it fills in an entry. But in
that case it takes O(n) time. There are O(n^2) entries to fill in,
so the total time of this memoizing dynamic program is O(n^3).
Finally, let's write a bottom up version that computes the answers in a simpler order. We have to be careful: it would not work to do for(i=1 to n) for(j=1 to n). For one thing, the problem only makes sense when j>i. But also, if we did it in that order we would need recursive values before they were computed. The whole idea of the simpler order is not to have to test whether a value has been computed, but instead to know because of the order that it already has been and just look it up. Here one idea that works pretty well is to compute in order of the difference d=j-i. So:
mtime(X)
{
array T[n,n]
for(d = 1; d <= n-1; d++)
for (i = 1; i <= n-d; i++)
{
j=i+d
if (j<=i+1) T[i,j] = 0
T[i,j] = +infinity
for (k = i+1; k <= j-1; k++) do
T[i,j] = min(T[i,j], T[i,k]+T[k,j]+X[i]X[j]X[k])
}
return T[1,n];
}
Now it's even more obvious that the total time is O(n^3): just look
at the three nested loops.
ICS 161 -- Dept.
Information & Computer Science -- UC Irvine
Last update: