The graph below is an example of a series-parallel graph (from the Wednesday, Week 7, notes on treewidth). Explain why the treewidth of this graph must be at least 2. (Hint: what can we say about the cliques in this graph?)
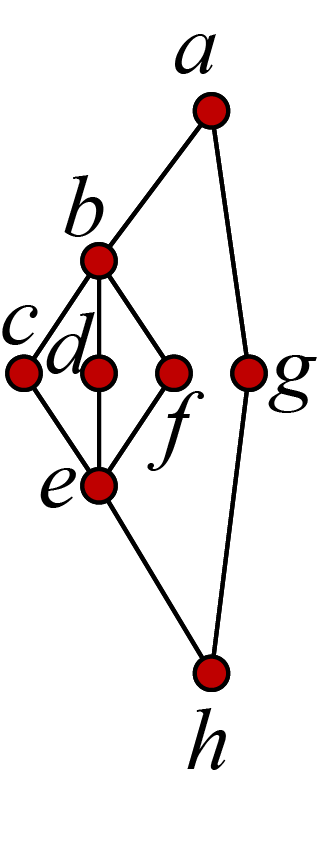
For the graph in Question 1:
This graph has minimal separators for the vertices \(a\) and \(h\) that are not cliques. Find such a separator.
Draw or list a set of additional edges that give a minimal chordal completion of this graph.
The figure below shows a path decomposition of the graph in Question 1.

Both classes: Suppose we run the fixed-parameter tractable coloring algorithm from the lecture notes on treewidth, using two colors: R and B. Consider the bag labeled "abe". Explain why, under the definition of "good" given in the algorithm, the following coloring is not good for this bag: \(a\): R, \(b\): B, \(e\): R.
265 students only: Describe a simpler algorithm for optimally coloring this particular graph. (Hint: is the graph 2-colorable? If so, what does this imply?)
The fixed-parameter tractable clique-finding algorithm from the slides uses the fact that every maximum clique in a graph is contained entirely in at least one bag of any tree (or path) decomposition for that graph.
163 students only: Is this also true for maximal cliques that are not maximum? Why or why not?
265 students only: Prove that this is true for tree decompositions. (Hint: we argued this for path decompositions in the lecture slides, using the two defining rules of a path decomposition. Generalize this reasoning.)