ICS 1F, Homework 4

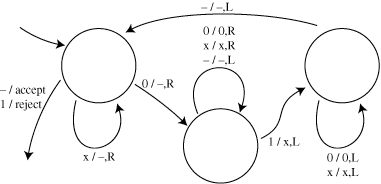
The circles in the following diagram represent the states of a Turing machine. An arrow labeled "a/b,D" means that if the machine sees the character "a", it replaces it by "b", moves in direction D (either left or right), and changes state as indicated by the arrow. An arrow labeled by "a/accept" or "a/reject" means the machine halts and accepts or rejects the string as indicated. The unlabeled arrow indicates the start state. A dash indicates the blank character.

1. Indicate for each of the following strings whether the machine above accepts, rejects, or goes into an infinite loop without halting: 01, 10, 011, 001, 0011.

2. Find a Turing machine that accepts strings of 0's and 1's only when the number of 1's is a power of two.

   (Hint: repeatedly pass left-to-right across the string to test whether there is exactly one "1" left, and right-to-left across the string changing every other "1" into a "0").

3. Why is it impossible to prove Church's thesis mathematically?