From:           baloglou@panix.com (George Baloglou)
Date:           31 Jul 1998 01:27:00 -0400
Newsgroups:     sci.math.research
Subject:        Polygons as projections of polytopes

The recent thread on "how to pixelize a sphere" (and related short tour of
polytopes) made me think of a question I posted on sci.math a couple of 
years ago but remained unnoticed at worst and unanswered at best:

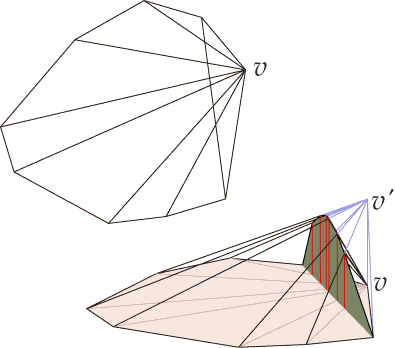
Is every convex polygon the projection of a polytope in such a way that
the polytope's vertices become the polygon's vertices and intersections of
diagonals, the polytope's edges become the polygon's edges and "diagonal
segments", and the polytope's faces become the polygon's "between-the-
diagonals" regions (save for the polytope's "base" that is the whole
polygon)?
 
For example, "lifting" the intersection point of a quadrilateral's two
diagonals vertically and "dragging" the diagonals along, we do get the
desired polytope (a pyramid); likewise, a "lifted diagonals' pentagon"
helps us solve the problem for n = 5, but it should by now be clear that
it is hard to generate the desired polytope for large n preserving both
the sought polytope's planarity of faces and the polygon's linearity of
diagonals (after projection). 

I arrived at this question when I became aware of a slick way of counting a 
polygon's "between-the-diagonals" regions using "Euler's polytope formula", 
r = e-v+2. [See for example Alan Tucker's "Applied Combinatorics" (2nd ed), 
p.184]

George Baloglou    baloglou@oswego.edu    http://www.oswego.edu/~baloglou

	"The Mathematics of our brain is not our Mathematics"

Date:           Mon, 16 Aug 1999 13:42:23 +1000
To:             baloglou@oswego.edu
From:           Andrew Kepert <andrew@frey.newcastle.edu.au>
Subject:        geometry junkyard
From:           Andrew Kepert <andrew@frey.newcastle.edu.au>
To:             baloglou@oswego.edu
Subject:        geometry junkyard
Date:           Mon, 16 Aug 1999 13:42:23 +1000

Hi George (& Cc: to David Eppstein)

Just browsing through the Geometry Junkyard, and found your posting
on polygons+diagonals being able to be lifted into a 3-d surface :
http://www.ics.uci.edu/%7Eeppstein/junkyard/diagonal-projection.html

>From:           baloglou@panix.com (George Baloglou)
>Date:           31 Jul 1998 01:27:00 -0400
>Newsgroups:     sci.math.research
>Subject:        Polygons as projections of polytopes
>
 . . .
>
>Is every convex polygon the projection of a polytope in such a way that
>the polytope's vertices become the polygon's vertices and intersections of
>diagonals, the polytope's edges become the polygon's edges and "diagonal
>segments", and the polytope's faces become the polygon's "between-the-
>diagonals" regions (save for the polytope's "base" that is the whole
>polygon)?
> 
 . . .

it is listed as "new" on the Junkyard, but it seems over a year old.  If you
haven't already found a solution, here is mine, firstly inductively,
then non-inductively.

Suppose you have, for an existing polygonal region P, a function
f giving the height at each point, being equal to 0 on dP, the
boundary of P and continuous and affine on the polygonal
subregions in question.  Add another vertex v, making a polygon Q.

Define g on Q to be that whose graph is a pyramid with
base Q and apex v.
[e.g. if x in Q\{V}, there is a unique lambda in [0,1] and
y in (dP intersect dQ) such that x=(lambda)v+(1-lambda)y.
Define g(x)=lambda.]
Then g+f is as required except on Q\P.

But this is easy to fix, as the diagonals passing through
Q\P divide it into triangles with a vertex at v.
[e.g. define h to have graph equal to the top surface of
the convex hull of graph( (g+f)|P ) union Q x {0} ,
OR define it as some lambda in a convex combination, as above]

Come to think of it, this construction can be done
in closed form.  Read a_b as a-subscript-b here:

Let P be the polygon and V the finite vertex set.
For each v in V, define g_v on P by
  g_v(x) = min{ lambda : exists y in P
                        such that x=lambda v + (1-lambda) y }
and define g = ( sum_v g_v ) - 1 .

Cheers, Andrew

[ Dr Andrew Kepert              e-mail: andrew@frey.newcastle.edu.au ]
[                               http://frey.newcastle.edu.au/~andrew ]
[ Central Coast Campus, Univ. of Newc., Ourimbah NSW 2258, AUSTRALIA ]
[                           Phone: 02 4348 4116    Fax: 02 4348 4145 ]
[ Mathematics, University of Newcastle, Callaghan NSW 2308 AUSTRALIA ]
[                           Phone: 02 4921 5190    Fax: 02 4921 5548 ]