For tetrominoes (shapes made from four squares), we can again just cut on the edges between squares. If we connect four squares by three appropriately placed hinges, we can form all five possible tetrominoes:
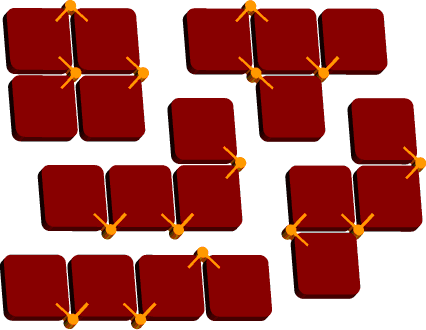
For higher-order polyominoes, the problem seems more difficult. For instance, it does not seem to be possible to join five squares by hinges and form all twelve pentominoes. However, we can still solve the hinged dissection problem by cutting the polyominoes into smaller pieces.
My original solution used the following "ambivalent square":
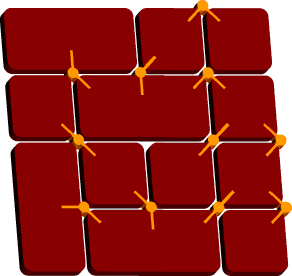
The figure shows twelve hinged pieces arranged to form a square. But because of the symmetric way in which the pieces are connected to each other, the same pieces can be folded into a square in a different way, in which the pieces at the top and bottom left corners of the figure have traded places. A connected sequence of 4k ambivalent squares forms a universal dissection that can be folded into any k-omino.
Erich Friedman then found a much simpler universal dissection: Just take 2k isosceles right triangles, hinged one to the next at their acute angles. So the straight pentomino could be made by 10 such triangles:
+--+--+--+--+--+
|1/|\2|3/|\4|5/|
|/0|9\|/8|7\|/6|
+--+--+--+--+--+
You can even join the ends to make a ring of triangles!
Erich and I now have a paper with Erik and Martin Demain, at the 1999 Canadian Conference on Computational Geometry: Hinged Dissections of Polyominos and Polyforms. In it, we describe this isosceles triangle construction, and related constructions for hinging polyiamonds, polyhexes, polyabolos, and similar shapes made from multiple copies of a single polygon.
From the Geometry Junkyard,
computational
and recreational geometry.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Last update: .