How can we test inscribability (or equivalently circumscribability)? Igor Rivin and Warren Smith gave a method of transforming the problem into a linear program. To test circumscribability, one places weights between 0 and 1/2 on each edge of the polyhedron, so that the weights on any face add to exactly one and the weights on any nonfacial cycle add to more than one. If this can be done, the polyhedron can be circumscribed. The edge weights have the following interpretation: multiplying each weight by 2pi gives the angle the edge would take up if viewed from the tangent points on either adjacent face. Dually, one can inscribe a polyhedron if and only if one can assign weights so that each vertex's weights add to one and each nontrivial cut (set of edges that separates two subsets of vertices) adds to more than one. (The meaning of these weights is harder to describe for inscription, but it can be related to the dihedral angles in a related problem of finding "ideal polyhedra" in hyperbolic geometry.) The existence of such a weighting system can be tested by applying the ellipsoid method for linear programming. However, it remains an interesting question whether there exists a more direct combinatorial method to check inscribability or circumscribability.
We might have more of a chance of finding such a method if we restrict our attention to special classes of polyhedra. One interesting special class of polyhedra are the 4-regular ones, in which each vertex is adjacent to exactly four edges. Since these graphs are Eulerian (equivalently, their duals are bipartite), every cut has at least four edges. There is a natural candidate for a Rivin-Smith weighting on these graphs: just give every edge weight 1/4. This might fail to work, if there exists a four-edge cut. However, one can then modify the weights by adding +epsilon and -epsilon alternately along the edges of an even-length cycle in the graph; this preserves the correct weights at the vertices, but might improve the weight of a cut. It turns out that any one cut can be made to have weight greater than one by such a procedure, so we might hope that repeating this procedure gives a correct weighting showing that 4-regular polyhedra are always inscribable. The only problem might be that making one cut have a better weight always is balanced by making another cut have a worse weight, so that no correct weighting exists. Can this happen? Yes!
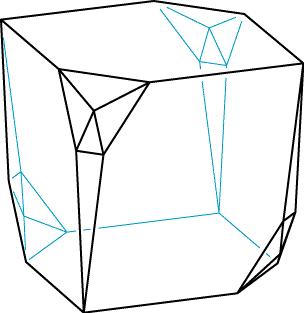
Mike Dillencourt and I formed the example above by replacing four of the vertices of a cube by gadgets derived from octahedra. To prove that this is not inscribable, we need to talk about a concept called "1-supertoughness". This has a scary name, but is actually a pretty simple concept: an n-vertex graph is 1-supertough if, whenever you remove some set of k vertices, the number of components you have left is at most k-1. The example above is not 1-supertough because, if you remove the four remaining unmodified cube vertices, you get four components. What does this have to do with inscribability? The weights on the removed vertices must be exactly one each, so the total weight of the edges between them and the rest of the graph must be exactly four. However, this means one of the four components must have weight at most one on the edges connecting it to the removed vertices, contradicting the assumption that a nontrivial cut has weight more than one. Therefore no weighting can exist and this polyhedron is not inscribable.
The following question remains open: is every 1-supertough 4-regular graph inscribable?
M. B. Dillencourt. Toughness and Delaunay triangulations. Discrete & Computational Geometry, vol. 5, no. 6, 1990, pp. 575-601.
M. B. Dillencourt and W. D. Smith. A linear-time algorithm for testing the inscribability of trivalent polyhedra. Proc. 8th ACM Symp. Computational Geometry, 1992, pp. 177-185. Int. J. Computational Geometry & Applications, vol. 5, 1995, pp. 21-36.
From the Geometry Junkyard,
computational
and recreational geometry.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Last update: .