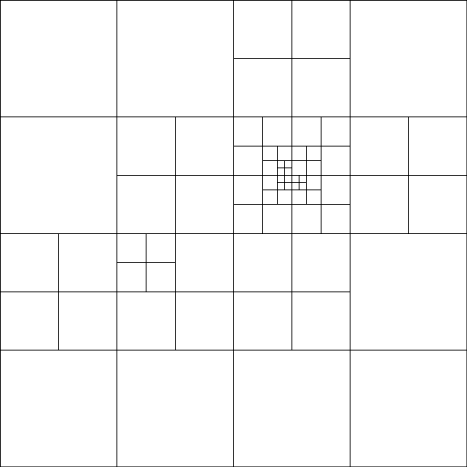
One drawback of circle packings, though, is that they seem to be very rigid: it is hard to change a small portion of a circle packing while leaving the rest of it alone. This is in contrast to some other geometric structures such as quadtrees, which are formed by repeatedly subdividing squares into quarters:

An advantage of the way quadtrees are constructed is that we can vary the local density: in some regions we can have very small squares, while other regions can be covered by very large squares. This is even possible while allowing relatively smooth gradations between adjacent squares (for instance only allowing a square to be adjacent to others between half and twice its size).
What I would like to discover is a similarly flexible structure for circle packings. Is there a way of constructing circle packings such that (1) each circle is tangent only to others within a constant factor of its size, and (2) if are given a sufficiently smoothly varying "local density function" f(x,y), the circle containing a point (x,y) has size proportional to f(x,y)?
It is possible to define circle packings that vary smoothly in one direction:
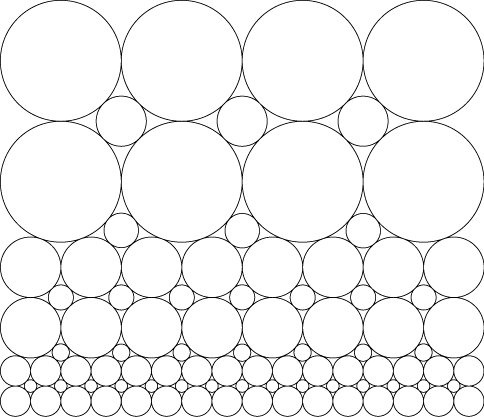
So e.g. if f(x,y) depends only on y, but not on x, the problem can be solved. What about more general local density functions?
While mathematicians have studied circle packings for some time, they have not been paid much attention by computational geometry, and one can also ask many other interesting questions about them. For instance, if we are given a finite collection of circles, how quickly can we determine whether they can be extended to a circle packing? Is this question even decidable?
See my web essay "Tangencies" for some basic techniques of constructing certain patterns of circle tangencies, that may be helpful in solving these problems.