MKL (s/d/c/z)GEMM: Banchmarking.

 

Matrix Multiplication is a basic kernel in Linear Algebra. MKL is one of the leading libraries for Intel architectures. Here, we present performance comparisons of the GEMM procedures for a DELL system based on a Pentium 4,  3.2GHz processor.

 

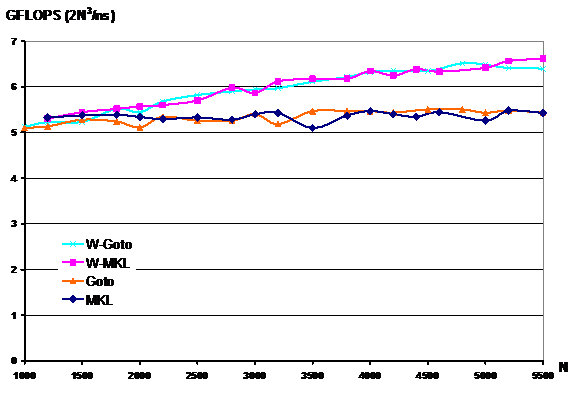
SGEMM: Single Precision General Matrix Multiplication

MKL SGEMM achieves up to 9 GFLOPS. Goto's SGEMM achieves up to 11 GFLOPS. If we apply our adaptive Winograd algorithm on top of MKL (W-MKL) and we normalize the performance using the formula 2N^3/nanoseconds, we achieve up to 10GFLOPS and on top of Goto's (W-Goto) we achieve up to 13GFLOPS. Notice that the peak performance for this application is 12.8GFLOPS. In practice, we achieve an execution time that is faster than any algorithm based on the classic N^3 algorithm.

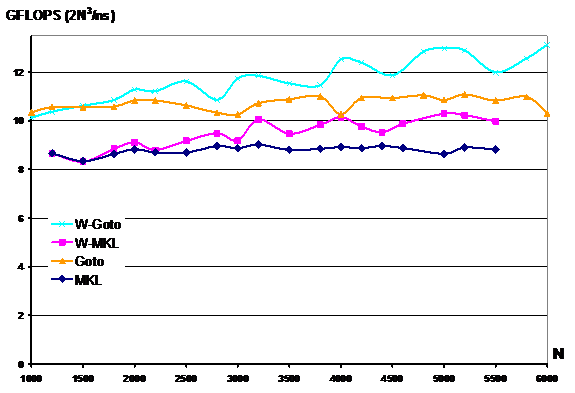
DGEMM: Double Precision General Matrix Multiplication

MKL DGEMM achieves up to 5.5 GFLOPS. Goto's SGEMM is slightly better for large problems and worse for small problems. If we apply our adaptive Winograd algorithm on top of MKL and Goto's and we normalize the performance using the formula 2N^3/nanoseconds, we achieve up to 6.5GFLOPS. Notice that the peak performance for this application is 6.4 GFLOPS. Once again, we achieve an execution time that is faster than any algorithm based on the N^3 algorithm.

 

CGEMM: Single-Precision Complex General Matrix Multiplication

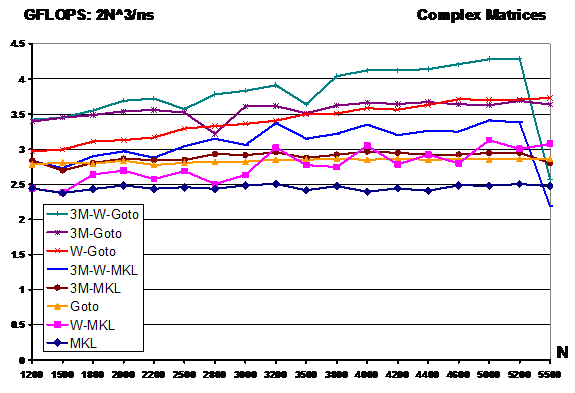
With complex elements, we have more options and most of these options have better performance than the one offered by MKL and Goto's.  Here we experiment with the 3M algorithm: This algorithm does not work on complex matrices, it splits a complex matrix into two single precision matrices and it performs 3 SGEMM (or DGEMM see below) and 4 Matrix additions (for a total of 25% operation saving). So we the term 3M-Goto, we identify the 3M algorithm using Goto's SGEMM. With the tern 3M-W-Goto, we identify the 3M algorithm applying our Winograd algorithm on top of the Goto's SGEMM.

 

MKL CGEMM achieves a peak performance of 2.5GFLOPS (normalized as 2N^3/ns). Goto's implementation achieves consistently better performance up to 2.8 GFLOPS. We can improve the performance of both by applying our Winograd, the 3M algorithm or both as shown in the performance plot above.  Using both 3M and Winograd algorithm applied to the three Goto's SGEMM (3M-W-Goto achieves up to 4.2 GFLOPS), we can achieve up to 40% execution time reduction w.r.t. MKL CGEMM. 

 

ZGEMM: Double-Precision Complex General Matrix Multiplication

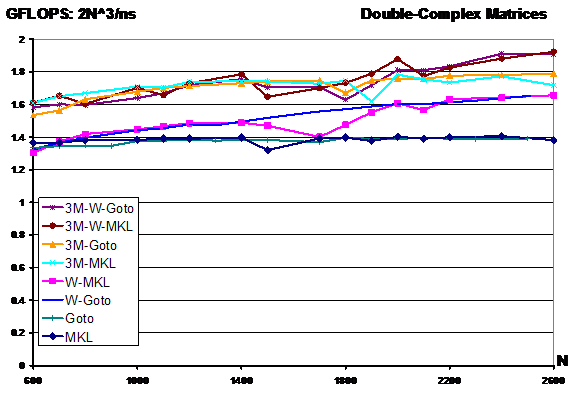
MKL and Goto's ZGEMM achieves a peak performance of 1.4 GFLOPS (normalized as 2N^3/ns). We can improve the performance of both by applying our Winograd, the 3M algorithm or both as shown in the performance plot above.  The 3M algorithm, instead of working on complex matrices, it splits a complex matrix into two single precision matrices and it performs 3 DGEMM and 4 Matrix additions (saving 25% operations). Using both 3M and Winograd algorithm applied to the three DGEMM, we can achieve up to 27% execution time reduction w.r.t. MKL ZGEMM.