Informatics 42 • Winter 2012 • David G. Kay • UC Irvine

Fifth Homework

Get your work checked and signed off by a classmate, then show it to your TA in lab by Monday, February 13.

Part I

Your local radio station wants to computerize its collection of CDs. They have asked you consider these three alternative data structures:

1. A conventional linked list, in no particular order
2. An array ordered by CD title, with an additional field that stores the number of CDs in the collection
3. A binary search tree, ordered by CD title.

When we ask for O-notations below, give the closest-fit O-notation in terms of n, the number of CDs n the collection, assuming each operation is coded as efficiently as possible in Java.

(a) Suppose the first task is to add all the CD data into the new system. Which of the three data structures would be most efficient for this task alone? As part of your answer, give each alternative's O-notation for adding a CD to the collection.

(b) A DJ spends most of his or her time looking up CDs by title. What is each data structure's O-notation for locating a CD by title? Which data structure do you most want to avoid for this task?

(c) The station manager wants to know at any given moment exactly how many CDs are in the collection. Give each alternative's O-notation for determining the number of CDs and say which alternative is most efficient for this operation. Don't assume the existence of any data fields not specified above.

(d) What would be the best data structure to use for implementing this collection, and (in one brief sentence including O-notations where appropriate) why? Assume that task (a) will be done just once and that most of the collection's usage will be split evenly between tasks (b) and (c). You may propose small modifications to the data structures described above if they would help produce a clear winner.

Part II

(a) As we did in class on Thursday afternoon, draw the state transition diagram (STD) for a finite-state automaton (FSA) that accepts the language of dollars-and-cents amounts with comas in the right places. Accepted strings include:

$1.00     $1,234.56      $1,234,567.89       $1,234,567,890.00
$13.27    $12,345.00     $12,345,678.90      $0.00
$125.50   $123,456.78    $123,456,789.00     $0.25

Rejected strings include:

$1        $5.000         $123,45.00          $1,234,00      $00.00
$25       $17.5          $1,234,5.67         $1,234,.00     $03.50
$234.     $1234.56       $1234,567.00        $,123,456.00   $0,123.45

(b) Below is some Python code that implements a kind of finite-state automaton.

SECRET1 = 35
SECRET2 = 127
SECRET3 = 33

stateList = [ "Init", "GotFirst", "GotSecond", "Success" ]

count = 1

state = "Init"

while state != "Success" and count <= 3:
    number = get_next()

    if state == "Init":
        if number == SECRET1:
            state = "GotFirst"
        else:
            state = "Init"
    elif state == "GotFirst":
        if number == SECRET2:
            state = "GotSecond"
        else:
            state = "Init"
    elif state == "GotSecond":
        if number == SECRET3:
            state = "Success"
        else:
            state = Init
    count += 1
    
if state == "Success": 
    print("Input accepted.")
else:
    print("Input rejected.")

(b.1) Draw the state transition diagram that represents the FSA this program implements. The input tokens here are whole integers, not individual characters.

(b.2) Describe in one brief English sentence what this FSA does. Try to think of a simple, real-world, non-computer-related object that this FSA models.

Intermezzo: State transition diagrams are one way to describe FSAs. Another way (which is easier to represent in a computer) is a transition table. A transition table has a row for each state and a column for each input (or each disjoint category of inputs); the value at each position in the table tells you what state to go to when you read a given input in a given state. Below is a transition table for the program above:

	Secret1	Secret2	Secret3	other
Init	GotFirst	Init	Init	Init
GotFirst	Init	GotSecond	Init	Init
GotSecond	Init	Init	Success	Init
Success

This table says just what the program and the state transition diagram say: If you're in Init and you read Secret1, you go into state GotFirst; if you're in state Init and you read anything else, you stay in Init. If you're in state GotFirst and you read Secret2, you go into state GotSecond; if you read anything else in state GotFirst you go to state Init. And finally, if you're in state GotSecond and you read Secret3, you go to state Success; otherwise, you go to Init. In state Success the machine stops, so you don't make any transitions out of that state; it's the accept state.

As we noted, transition tables make FSAs easy to represent in a computer. In fact, we can write a very simple but very general FSA simulator according to the following pseudocode:

initialize TransitionTable, ListOfAcceptStates 
state ← initial state

while there are more tokens:
    get a token;
    state ← TransitionTable[state][token];

if state in ListOfAcceptStates:
    accept
else:
    reject

Because this code is so simple, it's the preferred way to implement FSAs in programs. The only tricky part is finding a data type that will represent the range of tokens and will at the same time be acceptable as an array index in your programming language. Scheme, for example, handles symbolic names very easily, and so does Python, allowing any string to be an index into a dictionary.

(c) Think about the task of extracting words from a stream of text. In Python, you can use split() to divide lines around whitespace (or other separators), but sometimes you need to specify "words" idiosyncratically. You can do this kind of input-parsing task much more easily using state machines than by writing code directly.

(c.1) Draw a state transition diagram that accepts words defined as follows: a sequence of non-separator characters whose end is marked by a separator. Separators are symbols that separate English words—space, comma, semicolon, colon, and so on. Note that the hyphen (-), the apostrophe ('), and the percent sign (%) are not separators: treat "mother-in-law," "don't," and "23%" as single words. The end of the line is a separator, unless the last word of the line ends with a hyphen. That way, if a word like mother-in-law is hyphenated across two lines, it will still count as one word. (We will assume that in our input, only words that are always hyphenated will be hyphenated at the end of a line; that is, you should not expect normally-unhyphenated words to be broken across two lines.) Watch for multiple separators in a row—for example, a comma followed by a space is two separators, but there is no word between them.

You could code up this FSA into a method called getNextWord, and call it to parse a stream of input. Coding this isn't a required part of this assignment, though.

(c.2) Write a transition table for the state machine you drew in part (c.1).

(d) One of Scheme's attractions is that its syntax is very simple. Unlike Python, which has quite a few different statements, each with its own grammar and punctuation rules, every program or expression in Scheme is just a list of words surrounded by parentheses. This provides a rich variety of expression because a "word" can be (a) any sequence of characters delimited (separated from other words) by white space, or (b) a parenthesized list of words nested within the outside list. The following are all valid Scheme expressions (each is one line long except the last, which starts with the word define):

(Fee fie fo fum)
(+ 3.14159 1776 -45 quantity)
(equal? (+ 2 2) (+ 3 1))
(define square
  (lambda (x)
    (* x x)))

Novice Scheme programmers sometimes worry about keeping all the parentheses balanced, but most Scheme systems have "syntax-based" text editors that automatically keep track of the parentheses, so that any time you type a right parenthesis it automatically flashes the left parenthesis that matches it. That way you can see effortlessly what matches what. (This idea has found its way into some program editors for Python and other languages, where it's also useful.)

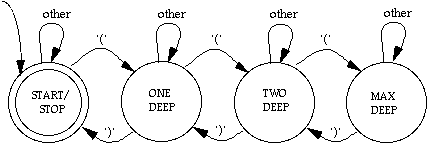
Suppose you decide to write a syntax-based editor for Scheme, and as your first task you want to write some code that checks whether the parentheses are balanced in a Scheme expression. Astutely, you start by designing an FSA. To make it truly a finite-state machine, we have to put an upper limit on the depth to which parentheses can be nested; the example below shows the FSA for an upper limit of three-deep nesting. (In the diagram, "other" means an input symbol other than an open or close parenthesis.)

(d.1) After scanning the entire Scheme expression, in what state should your machine be if the parentheses were correctly balanced?

(d.2) This FSA works fine in theory, but for a realistic nesting depth of a few dozen, the diagram would be tediously repetitious. So you decide to simplify things and encapsulate the state information in a simple integer counter. Then you can have a single state on the page, and all the action happens in the transition steps, where you increment the counter for each left parenthesis and decrement it for each right parenthesis. [Having a variable may appear to violate the definition of a finite-state machine, all of whose information is encapsulated in a finite number of states. But since integer variables on computers (as opposed to integers in mathematics) always have a finite upper bound, we're technically safe. If our machine used a stack to keep track of the unbalanced parentheses (which is what our integer counter is modeling), it would no longer be an FSA—it would be a PDA (push-down automaton), which can accept a broader class of languages.]

The modified (augmented) machine appears below.

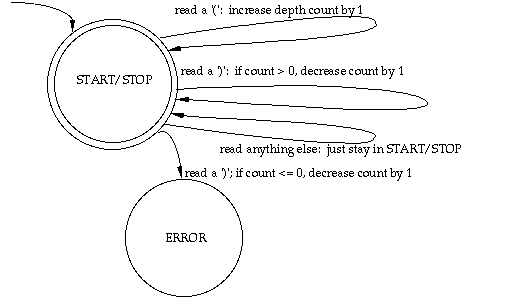
(d.3) Things are rarely quite as simple as they first seem. Comments in Scheme programs start with a semicolon and extend to the end of the line. Thus, the following is a valid Scheme expression; everything to the right of the semicolon on each line is a comment. Of course the contents of comments are ignored when checking for balanced parentheses.

  (define print-it        ; In this routine we
    (lambda (p)           ; a) accept a parameter,
      (display p)         ; b) display it, and
      (newline)))         ; c) hit carriage return

Draw a new FSA-like machine, similar to the one above, to account for comments correctly; you will have to add more states.

(d.4) And there's one more wrinkle. Literal character strings in Scheme are enclosed in double-quote marks. As in any programming language, the contents of literal strings are ignored when analyzing the syntax of the program. The following three expressions are valid in Scheme.

(display "Oh; really?") 
(list  "a)"  "b)"  "c)" ) 
(let ((delims ".,;:)(("))) ; This has an extra '(' in quotes

Draw a new FSA-like machine to handle both strings and comments correctly.

(d.5) Write a transition table for the state machine you designed in part (e.4). Note that some of the transitions in some conditions will also increment or decrement the count of parentheses.

(d.6) Test your FSA from part (e.4) thoroughly on paper—devise a thorough test plan and work each test through your FSA.

(e) (Optional) Available on the web is a program called JFLAP, written at Duke University (http://www.jflap.org/). You can download this Java application and use it to build and test your own simple FSAs (as well as do other formal-language activities). Other state machine simulators are available on the web; you can find some of them by using search strings like "state machine applet" or "FSA animation."

Written by David G. Kay, Winter 2005.

FSA exercises written by David G. Kay, Winter 1991 (based on materials from 1990 and earlier). Revised by Joe Hummel, Norman Jacobson, Theresa Millette, Brian Pitterle, Alex Thornton, Rasheed Baqai, Li-Wei (Gary) Chen, and David G. Kay, 1992-1999.

Modified by David G. Kay to reflect Python, Winter 2012.