Tree Processing: Iterative and Recursive

Introduction to Computer Science II
ICS-22

In this lecture we will continue our study of trees by examining ordered binary search trees and various method for processing them (methods useful for storing collections in trees). After discussing a required ordering property, we will examine how to search such trees in time proportional to Log₂N (where N is the size of a reasonably perfect search tree); we will also discuss how to add and remove values from a tree. Finally, we will examine how to recursively traverse trees and study three standard traversal orders, and some of their applications.

Ordered Binary Search Trees (BST)

For a binary tree to be quickly searchable it must satisfy a simple ordering property: the value stored at any node must be greater than each value stored in its left subtree and smaller than each value stored in its right subtree. This property is not just true for the root, but it must be true for every node in the tree; it is trivially satisfied for leaf nodes, because they have empty left and right subtrees. The following example illustrates an ordred binary search tree storing int values (constructed from the TN class defined in the previous lecture).

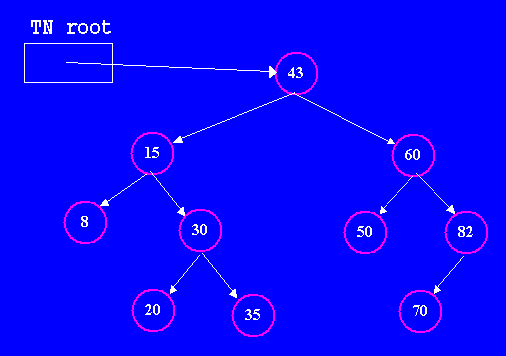
Notice that the ordering property is true for each node (check it). We will abbreivate such trees as just binary search trees (or BST) with the implication that they must adhere to this standard ordering property to be quickly searchable. If any tree fails the ordering property, it means that we can find a specific node in that tree whose left or right child is not appropriate: whose value is not ordered correctly when compared to the value stored in its parent.

In a later lecture we will learn of another way to "order" the values stored in a binary tree. A heap ordering requires that every node be bigger than each node in its subtree; this ordering property does NOT allow for quick searching in a tree, but it does allow us quickly to insert any value and remove the largest value (two operations that are necessary to implement a priority queue efficiently). We will study heaps in more detail in the next lecture.

For now, understand that there are multiple ways to order trees, and the standard ordering property is useful when we need to create quickly searchable binary trees.

Throughout this lecture we will assume unique values stored in the BST. There are two standard ways to implement BSTs with identical values.

Store a counter (initialized to 1) to record how often a value appears.
Treat a duplicate value no differently than any other value when inserting; the code given below stores each duplicate value to the right of each value already occuring in the tree.

Searching Ordered Binary Search Trees

The ordering property supplies us with all the information that we need to search binary trees quickly, where each decision (telling whether to stop, or search the left or right subtree) depends only on the value stored in the node that we are currently examining:

if the value we are searching for is equal to the value in the node, we have found the node
if the value we are searching for is less than the value in the node, we search the left subtree
if the value we are searching for is greater than the value in the node, we search the right subtree

By the law of trichotomy, exactly one of these relationships must hold between every pair of values. Such tests are easy to perform on primitive types by using relational operators; classes that support trichotomous comparisions typically implement the Comparable interface, which defines a compareTo method that returns a negative, zero, or positive value to distinguish less than, equal to, and greater than (e.g., see the String class). The Comparator interface also generalize these kidns of comparisons.

We can write methods that implement this searching algorithm either iteratively (because we only examine one subtree) or recursively (we recursively explore either the left or the right subtree, but never both). First, here is an iterative method (there are lots of variants equivalent to this one, depending on how the for loop is written).

  public static TN locate (TN root, int toFind)
  {
    for (TN c=root; c!=null; c = toFind<c.value ? c.left : c.right)
      if (toFind == c.value)
        return c;

    return null;
  }

Next, here is a recursive method to implement this same algorithm. Although this method is a bit more complicated to write than the iterative one, the pattern of recursive calls it uses is repeated when writing various insertion methods (one of which appears below).

  public static TN locate (TN t, int toFind)
  {
    if (t == null)
      return null;
    else
      if (toFind == t.value)
         return t;
      else if (toFind < t.value)
         return locate(t.left, toFind);
      else
         return locate(t.right,toFind);
  }

Notice that the statement in the final else has no test: if the equality test failed, and the less-than test failed, it must be the case (by the law of trichotomy) that toFind is greater than t.value, so no explicit test is needed.

Sometimes programmers simplify this method a bit and write it as follows, combining the "empty tree" and "found" cases, as

  public static TN locate (TN t, int toFind)
  {
    if (t == null || toFind == t.value)
      return t;
    else
      if (toFind < t.value)
         return locate(t.left, toFind);
      else
         return locate(t.right,toFind);
  }

In all three methods, we traverse only the parts of the tree that can possibly contain the value we are searching for, moving down one depth at each unequal comparison, until we either reach the node that we are searching for (an == comparison), or an empty (null) subtree.

We can prove that the recursive method is correct as follows.

For the base case (an empty tree) this method returns the correct value: null (not found, becuase no values can be found in an empty tree).
The recursive calls are applied to a strictly smaller tree (at least one fewer nodes and of at least one smaller height: both integers that characterize the size of a tree/problem).
If we are referring to a node, we can assume locate(t.left,toFind) and locate(t.right,toFind) correctly return a reference to a node whose value is toFind in their subtrees, if it is there. Now, if t.value is toFind we return it immediately without searching further; if not we call this method on the appropriate subtree where it would, if present, be (the other one, by the ordering property, cannot contain toFind), and just return its result.

Finally, note that in the worst case, we have to visit one node at every depth in the tree. Thus, the complexity class of these methods is best characterized as O(height); but also note that we have learned that in a well balanced tree the height is O(Log₂size), so for an N node tree (size = n), the complexity class of searching is O(Log₂N). For well balanced trees (as close to perfect as possible), whenever we explore one subtree we disregard its sibling, so we cut the number of nodes we must search in half each time we descend the tree. Thus, binary search trees are a self referential structures that we can search may be able to search as quickly as sorted arrays (and more quickly than unsorted arrays or linear linked lists).

Now let's discuss how build such trees, by insertion.

Insertion and Deletion in Ordered Binary Search Trees

To insert a value into a binary search tree we follow a similar process to searching: ultimately we will insert the value as a new leaf node in the tree (where the value would be found if we were searching for it in the tree). In this way, trees grow at their fringes. Although we can write this method iteratively (and you are certainly invited to do so), the recursive implementation is much much simpler. It uses a pattern similar to, but generalizing, insertion in linear linked lists (review that code if you have forgotten it; you should be able to reproduce it).

  public static TN insert (TN t, int toInsert)
  {
    if (t == null)
      return new TN(toInsert,null,null);
    else {
      if (toInsert < t.value)
         t.left  = insert(t.left, toInsert);
      else
         t.right = insert(t.right,toInsert);
      return t;
    }
  }

This method replaces l.next = insert(l.next,toInsert) by two calls doing the equivalent with the left and right subtree references. We call this method like root = insert(root,5);

Because it is so similar to searching a tree, this method also has the same complexity class, at most traversing every depth in the tree before correctly placing the new value to insert. Also note that if a binary search tree is ordered before insertion, it is still ordered after insertion (the new value goes into a node that etends the tree in exactly the spot it belongs in a BST).

Note an important fact: there are many structurally different ordered binary search trees containing exactly the same values; the structure of the tree is dictated by the order in which the values are inserted in the tree (the first is root, and the rest depend on the root). For example, here is a ordered binary search tree that contains the same values as the one above, but is structurally very different.

In fact, if we inserted values into this tree in increasing order, we would end up with a pathological republican tree.

We have seen that the height of a binary tree must be at least Log₂(size+1) - 1 (for perfect trees) and at most size-1 (for pathological trees). In the upcoming programming project, you will repeatedly build trees by inserting values from a permutation of integers 1 up to N, and then compute their height (and eventually computing the average height for all trees you build). Then you will double N and repeat the process. Finally, you will determine an approximate formula for the average height of a tree with N nodes.

There is an iterative method that we can use to insert a node into a binary search tree that already has a root node (so that case must be taken care of specially, not in this method).

  public static void add (TN t, int toInsert) {
    for (;;)
      if (toInsert < t.value) {
        if (t.left == null) {
          t.left = new TN(toInsert,null,null);
          return;
        }
        t = t.left;
      }else{
        if (t.right == null) {
          t.right = new TN(toInsert,null,null);
          return;
        }
        t = t.right;
      }
  }

Note in this code, if the value belongs to the left/right of a node, we must check to see if nothing is there (in which case we add the node there and are done); if there is something there, we just advance the t reference to the left/right and continue. Although the recursive locate/add look similar, the iterative locate/add are quite different.

Deleting a value from a binary search tree is a much more complicated and delicate operation. We can describe the algorithm fairly simply (it is still more complex than most), but it is difficult to implement concisely and efficiently. People can follow this algorithm much more easily than the Java method that implements it, so we will focus only on the algorithm here.

To delete a value from a BST:

Find the node containing the value to be deleted
If it is a leaf, remove it: make the reference from its parent instead refer to null
If it is an internal node with one child, make the reference from its parent instead refer directly to its only child
If it is an internal node with two children
- Find the node containing either the largest value smaller than it or the smallest value larger than it (it doesn't matter which)
- Remove that node from the tree (it is guaranteed to have at most one child, so it will be easy to delete)
- Replace the value of the original node (the one to delete) with the value of this node (just deleted)

Removing a leaf node leaves the ordering property intact. Removing a node with one child does likewise: all the nodes descending from the removed node compare against its parent in the same way. Finally, when we replace a node with two children by either its smallest larger descendent or its biggest smaller descendent, all its descendents compare the same way. Thus, removing a node from an ordered binary tree leaves the tree still obeying the ordering property.

Here is the code (two methods) for removing a value from a BST.

  
  public static TN lift(TN t, TN toRemove)
  {
     if (t.right == null) {
       toRemove.value = t.value;
       return t.left;  
     }else {
       t.right = lift(t.right,toRemove);
       return t;
     }
  }
  
  
  public static TN remove (TN t, int toRemove)
  {
    if (t == null)
      return null;
    else if ( toRemove == t.value ) {
       if (t.left==null)
         return t.right;
       else if (t.right==null)
         return t.left;
       else{ 
         t.left = lift(t.left,t);
         return t;
       }
    }else{
      if ( toRemove < t.value )
        t.left  = remove(t.left,toRemove);
      else
        t.right = remove(t.right,toRemove);
      return t;
    } 
  }

For this course, you are expected to know how to construct a BST by inserting values, and to show the result of removing a value from a BST. You should know how to do this quickly. You are also responsible for understanding (and being able to write) the code for searching and insertion in BSTs (but not the code for deletion; on the other hand, you should be able to adapt this deleteion code so that it works for any type of the value instance variable).

Traversals in Ordered Binary Search Trees

We have already covered searching for values in BSTs, inserting values in BSTs, and deleting values in BSTs. We will now discuss processing all the nodes in a binary tree by traversing the tree. Generally, we will process the value in a node when we visit it, and then process every value in the node's left and right subtrees. There are three standard traversal orders, each relating when a node's values is processed compared to when the values in its subtrees are processed. The three traversal orders are:

Preorder: process the value in the current node first, then its left and right subtrees.
Inorder: process the left subtree first, then the value in the current node, then its right subtree.
Postorder: process the left and right subtrees first, then the value in the current node.

Thus, the traversal order is determined by when a node's value is processed compared to when the values in its subtrees are processed: pre (before), in (in between), and post (after).

As a simple example, suppose that we want to visit every node in the tree and print its values. The following simple method does so with a preorder traversal.

  public static void printPreorder (TN t)
  {
    if (t == null)
      return;
    else {
      System.out.print(t.value);
      printPreorder(t.left);
      printPreorder(t.right);
    }
  }

For an inorder traversal the print statement would instead come between the recursive calls. For a postorder traversal the print statement would instead come after both recursive calls.

Breadth-First traversals process all the nodes at one depth before descending to the next one. There is no simple recursive methods for this kind of traversal: instead, we use a queue and loop to do the job.

  public static void printBreadthFirst (TN t)
  {
    AbstractQueue q = new LinkedQueue();
    q.add(t);
    for (;!q.isEmpty();) {
      TN next = (TN)q.remove();  //cast from Object
      if (next != null) {
        System.out.print(next.value);
        q.add(next.left);
        q.add(next.right);
      }
    }
  }

Note that in this method, many null values get enqueued and then ignored when they are dequeued. We could write a slightly more complicated version of this method that avoided doing so.

Here is the original BST and the order it would print its values using each traversal order.

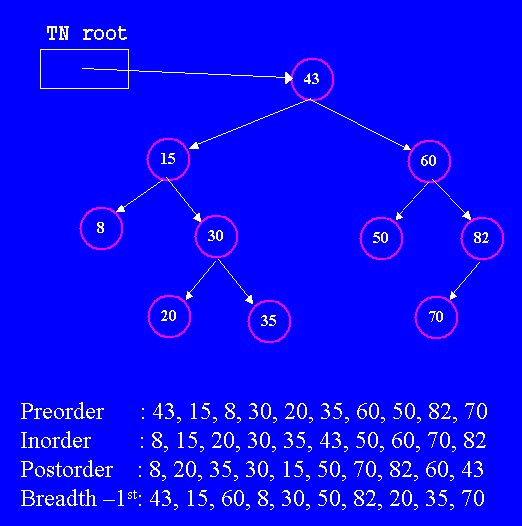
Notice that inorder traversals print the node values in sorted order (according to the ordering property). Also notice that preorder traversals print the node values in such an order that by inserting nodes in an empty tree in this order we build the original binary tree: parents are always inserted before their children. Thus, we can write a BST out to a file and read it in to rebuild exactly the same binary tree. We will discuss a standard uses of postorder traversals when we discuss evaluating expression trees in the next lecture.

Problem Set

To ensure that you understand all the material in this lecture, please solve the the announced problems after you read the lecture.

If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a TA, or any other student.

Write an int method named min, which returns the minimum value stored in a binary search tree. What is the complexity class of this method?
Write a copy method, which takes a TN as a parameter and returns a TN as a result (a reference to a copy of the tree).
Write a boolean method named isBST that returns whether or not its TN parameter is an ordered binary search tree; you will need to write a helper method (or tow) to check the ordering property. What is the complexity class of this method?
Write a method named named nicePrint that prints its TN parameter nicely, such that the tree at the top of this handout prints as 82 70 60 50 43 35 30 20 15 8
Hint: add a second parameter that is a String with the amount of space necessary to print the value at this node with the right indentation. What is the complexity class of this method?
Write a method called buildBalancedBST which takes an int[] as a parameter and returns a reference to the root of a reasonably well balanced BST. Hint: you should write one (or more) helper methods. Because arrays cannot be decomposed into smaller arrays, pass two parameters specifying the lowest/highest index in the array to process.
Examine the alternative BST and show what order it would print its values using each traversal order. What is the complexity class of each traversal method?

Tree Processing: Iterative and Recursive

Introduction to Computer Science II ICS-22

Introduction to Computer Science II
ICS-22