The answers
Problem 1
Results on this problem were mixed, with an average score of 4.6 out of 8. Many people lost a point on the first part, as they didn't answer the question that was asked. Several others didn't write regular expressions, but instead wrote grammars or some other kind of notation that we couldn't unscramble.
a)
The answers here were:
| Version A | Version B | Version C |
| a+b+ | x+y+ | y+x+ |
Other equivalent regular expressions, such as aa*bb* were accepted, as well. The most common wrong answer was one of the form ab+, which was awarded half-credit.
b)
There are certainly multiple reasonable solutions to this problem (which mimicked a problem you faced on one of the lab assignments), but straightforward answers were:
| Version A | Version B | Version C |
| [A-Z] [a-z]* ($ [A-Z] [a-z]*)* | [A-Z] [a-z]* (- [A-z] [a-z]*)* | [a-z] [A-Z]* (^ [a-z] [A-Z]*)* |
Other answers that were equivalent were accepted. Of the three points possible, one was allocated to the first part (building one word) and two more were allocated to the second part (the subsequent words, separated by the appropriate character).
c)
Again, more than one answer was acceptable here. Some students used JFlex-style shorthands; if we could decipher them (i.e. they were clear and were not recursive!), we still tried to award credit when we could. This question was the same on all three versions, and one possible good answer was:
| All Three Versions |
| (0 | [1-9] [0-9]*) (. (0 | [0-9]* [1-9]))? |
Problem 2
This problem asked for the output of a JFlex script, given a set of patterns with actions that called System.out.println. It essentially tested whether you understood the greedy matching algorithm used by JFlex (i.e. one that always takes the longest possible match). By and large, students did very well on this question, averaging 4.5 out of 6 points.
Roughly speaking, one point was deducted for each kind of mistake found, such as matching substrings of a-e and 1-5 separately, not matching the longest one, etc. Also, 1 point was deducted for an output format not matching the requirements, such as a long sequence of numbers (e.g. "245341353").
The JFlex script was the same on the three versions, though the input strings were different. The correct answers were:
| Version A | Version B | Version C |
|
2 abcd 4 77 5 cabc234 3 Q 4 7 1 abc 3 J 5 3c2a1 3 H |
2 abcd 4 00 5 babc123 3 Z 4 0 1 abc 3 G 5 5a3b4 3 F |
2 abcd 4 99 5 cbab234 3 V 4 9 1 abc 3 F 5 4b2c3 3 G |
Problem 3
By and large, students did pretty well on the first part and not well at all on the second part. The average score overall on the problem was 4.5 out of 8.
a)
The three versions differed only in terms of the regular expression that appeared in part (a), though all three regular expressions were of a similar form, so I'll just show the answer for one of the versions (for which the regular expression was a | (bc)*). Since the problem specifically asked you to use Thompson's construction, equivalent NFA's (i.e. NFA's that are different -- including DFA's! -- but accept the same language) were not accepted.
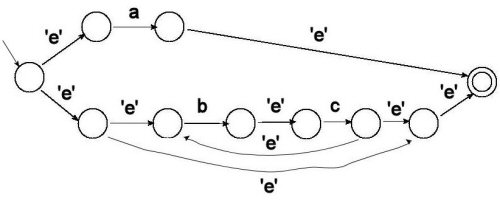
b)
This part of the problem was the same on all three versions. Since the problem specifically asked you to use the subset construction to build the DFA, equivalent DFA's (i.e. DFA's that are different but accept the same language) were not accepted. Naturally, NFA's were not accepted either. State names were not considered relevant.
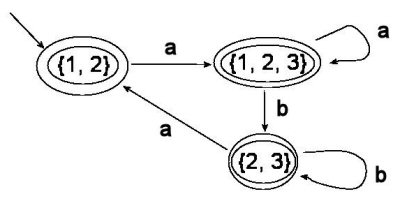
It should be pointed out that, even though all three of this DFA's are accept states, it still doesn't accept all strings. Strings such as b or abab are not accepted by it.
Problem 4
Answers for this problem (which I graded myself) were all over the map. The average score on it was 3.9 out of 8, with a substantial portion of that coming from part (a). Part (b) was a disaster, but it was a great deal more difficult than I'd originally intended.
a)
This problem had a wide variety of answers, many of which were clearly not LL(1). Many students tried a variety of transformations that don't make any sense, such as flip-flopping rules like Y → Ybc to Y → bcY. More than one answer was considered correct, but it had to be an LL(1) grammar that accepted the same language.
The straightforward answer, which you could arrive at by performing the transformations we discussed in class on the original grammar, was:
| Version A | Version B | Version C |
|
X → Ya | Zbc Y → abaY' | cabaY' Y' → bcY' | ε Z → bZ' Z' → bc | c |
A → Bx | Cyz B → xyxB' | zxyxB' B' → yzB' | ε C → yC' C' → yz | z |
D → Er | Fst E → rsrE' | trsrE' E' → stE' | ε F → sF' F' → st | t |
Partial credit was given for transforming portions of the grammar correctly, even if the entire grammar was not LL(1). Students were much more commonly able to transform Z → bbc | bc to Z → bZ' and Z' → bc | c than they were able to perform the left recursion elimination on Y correctly.
b)
This problem actually couldn't be solved using strictly the techniques shown in class. For that reason, I accepted some answers that were arrived at by applying as many of these transformations as could be applied, even if the final grammar was not LL(1). (Few students got this far, as it turned out, and the most common score on this part of the problem was 1 out of 4, awarded for attempting to perform some kind of transformation to the grammar.) A few students applied some ingenuity, reverse engineering the grammar and building a new one. After inspecting the behavior of the grammar, you can discover that the grammar describes a language that can be described by the regular expression ab (bb | cb)*, from which you can build a grammar.
The incorrect but acceptable answer looked like this:
| Version A | Version B | Version C |
|
X → Yb Y → aY' Y' → ε | bY'' Y'' → bY' | cY' |
A → By B → xB' B' → ε | yB'' B'' → yB' | zB' |
D → Es E → rE' E' → ε | sE'' E'' → sE' | tE' |
(These grammars are not LL(1) because, for example, starting with this derivation: X ⇒ Yb ⇒ aY'b ⇒ ...it is not clear now, with the next character of input being a b, whether we should expand by Y' → bY'', or by Y' → ε.)
Correct answers looked like one of these grammars (or something very much like them):
| Version A | Version B | Version C |
|
X → abY Y → bbY | cbY | ε or X → aY Y → bY' Y' → ε | bbY' | cbY' |
A → xyB B → yyB | zyB | ε or A → xB B → yB' B' → ε | yyB' | zyB' |
D → rsE E → ssE | tsE | ε or D → rE E → sE' E' → ε | ssB' | tsB' |
The answers are inspired by two different regular expressions: ab (bb | cb)* and a (bb | bc)* b.
Problem 5
After the homework assignment I gave on this topic, students seem to have gotten the point about FIRST and FOLLOW sets. The average score on this problem was 7.8 out of 9.
a)
The first five sets had only one element each; they were worth a total of one point. The others were worth one point each.
| Version A | Version B | Version C |
|
FIRST(ε) = { ε } FIRST(a) = { a } FIRST(b) = { b } FIRST(c) = { c } FIRST(d) = { d } FIRST(S) = { b, c, d, a, ε } FIRST(X) = { b, c } FIRST(Y) = { d, a, ε } |
FIRST(ε) = { ε } FIRST(x) = { x } FIRST(y) = { y } FIRST(z) = { z } FIRST(w) = { w } FIRST(S) = { y, z, w, x, ε } FIRST(A) = { y, z } FIRST(B) = { w, x, ε } |
FIRST(ε) = { ε } FIRST(r) = { r } FIRST(s) = { s } FIRST(t) = { t } FIRST(v) = { v } FIRST(S) = { s, t, v, r, ε } FIRST(D) = { s, t } FIRST(E) = { v, r, ε } |
b)
Results were strong here, too, with some of the most common mistakes being including ε and not including eof. These were worth one point each.
| Version A | Version B | Version C |
|
FOLLOW(S) = { eof } FOLLOW(X) = { eof, d, a } FOLLOW(Y) = { eof, c } |
FOLLOW(S) = { eof } FOLLOW(A) = { eof, w, x } FOLLOW(B) = { eof, z } |
FOLLOW(S) = { eof } FOLLOW(D) = { eof, v, r } FOLLOW(E) = { eof, t } |
c)
This was worth two points, all or nothing. The answer was Yes!!! (though the exclamation marks were not required :) ).
Problem 6
Students didn't do particularly well on this question, with the average score being 4.4 out of 9. As with most other questions on the exam, a wide variety of answers were given.
For all three parts of the problem, the following rubric was used for grading (and marks were made accordingly with the notation shown in parentheses):
- -0.25 points for each wrong or missing lookahead (WL / NL)
- -1 point for not computing the closure of a set (NC)
- -0.5 points for missing an item in a set (MI)
- -2 points for a wrong set of LR(1) items in part b (TWS, WS)
- -1 point for missing the first item in goto in part b (MFI)
- -2 points for missing first set of LR(1) items in part b (N1S)
- -2 points for missing second set of LR(1) items in part b (N2S)
- -2 points for missing third set of LR(1) items in part b (N3S)
- If many more items than needed were listed, no credit was given.
a)
The initial state of the parser consisted of six LR(1) items. Each was worth a half-point.
| Version A | Version B | Version C |
|
{ [Goal → • S, eof], [S → • YY, eof], [Y → • fY, f], [Y → • fY, g], [Y → • g, f], [Y → • g, g] } |
{ [Goal → • S, eof], [S → • BB, eof], [B → • eB, e], [B → • eB, f], [B → • f, e], [B → • f, f] } |
{ [Goal → • S, eof], [S → • EE, eof], [E → • gE, g], [E → • gE, h], [E → • h, g], [E → • h, h] } |
b)
If we apply goto to Sz, we can reach three distinct parse states.
| Version A | Version B | Version C |
|
goto(Sz, Y) = { [S → YY •, eof] } goto(Sz, f) = { [Y → f • Y, eof], [Y → • fY, eof], [Y → • g, eof] } goto(Sz, g) = { [Y → g •, eof] } |
goto(Sz, B) = { [S → BB •, eof] } goto(Sz, e) = { [B → e • B, eof], [B → • eB, eof], [B → • f, eof] } goto(Sz, f) = { [B → f •, eof] } |
goto(Sz, E) = { [S → EE •, eof] } goto(Sz, g) = { [E → g • E, eof], [E → • gE, eof], [E → • h, eof] } goto(Sz, h) = { [E → h •, eof] } |
Problem 7
This problem was thrown out, as it had at least one mistake on every version, and at least one more mistake on at least one of the versions. Ugh!