---

Ordering what's stored in a binary tree

The N-ary and binary trees that we saw previously are not, themselves, especially interesting. They form the basis of solutions to some interesting problems, but without additional care, they aren't sufficient to solve any particular problems. But we can use what we know about their structure to create clean, performant solutions to problems, if we can make some additional decisions about how to organize our data into the tree. What do we store where? What other guarantees do we need to make about the shape of the tree, besides just how many children each node might have?

We'll explore one such application of binary trees here, as we use their structure to help us organize information so that we can search for it efficiently later. Along the way, we'll discover that we're only better off if we're careful about how we use them; we'll need to understand the ways in which they behave badly, so that we can then work on ways of avoiding those situations.

---

Binary search trees

First, let's consider the following definition:

A binary search tree is a binary tree in which every (internal) node stores a unique key. For every node n containing a key k:

• All of the nodes in n's left subtree have keys smaller than k
• All of the nodes in n's right subtree have keys larger than k

So, generally, a binary search tree is a binary tree containing keys (and possibly values associated with those keys). There are limitations on where the keys are allowed to reside, so that if we're ever looking at a given node that contains some key, we can be certain that every node in its left subtree will have keys that are smaller, and every node in its right subtree will have keys that are bigger. Of course, binary search trees don't just fall out of the sky already organized this way; it'll be up to us to maintain this property whenever we add or remove keys, and in that lies a lot of the challenge. But once we have a binary search tree, as we'll see, finding keys (and their associated values) becomes surprisingly simple and, more importantly, can be very fast indeed, even for very large collections of keys.

It's important to note that the keys must have a meaningful ordering. Integer keys could be ordered smaller-to-larger; string keys could be ordered alphabetically or lexicographically; and so on. For simplicity, we'll demonstrate binary search trees using only integer keys, but the keys can be anything, as long as there's an unambiguous way to order them.

An example of a binary search tree is pictured below.

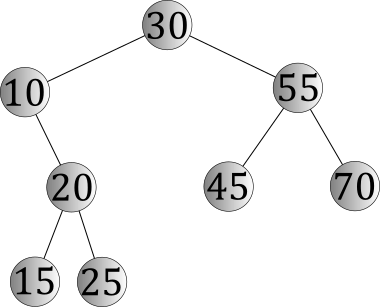
What makes this a binary search tree is that it fits both of the necessary properties of the definition:

• It is a binary tree. Every node has exactly two subtrees, though some of them (such as 10's left subtree) are empty.
• The keys are ordered according to the data-ordering property; no matter what node you choose, all of the keys in that node's left subtree are smaller and all of the keys in that node's right subtree are larger.

Lookups in binary search trees

The lookup operation in a binary search tree is one that finds out whether a particular key is in the binary search tree somewhere; if so, and if there is a value associated with it, that value might also be returned, but the general behavior — how we find the key — is the same regardless.

Because we know how the keys are organized — in particular, that smaller keys will only be found in left subtrees and larger ones will only be found in right subtrees — we can do this job surprisingly well. For example, suppose we lookup the key 25 in the binary search tree above. We would follow this sequence of steps.

• Begin by looking at the root node, which contains the key 30. Since 30 isn't the key we're looking for, we haven't found it. But since the key 25 is smaller than the key in the root node, we're sure that one of two things is true: (1) the key 25 is in the left subtree of the root, or (2) the key 25 is nowhere to be found.
• Armed with this knowledge, we proceed to the left child of 30, in which we find the key 10. 10 isn't 25, either, but we do know that 25 is larger than 10; so the key 25, if present, will be in 10's right subtree.
• Continuing on, we look at 10's right child, in which we find the key 20. 20 isn't 25, but 25 is larger, so we should proceed to the right.
• Finally, we reach 20's right child, in which we find the key 25 that we were looking for.

If we had instead been searching for the key 27, note that we would have followed all the same steps, with the only difference being that we would have reached the node containing 25, concluded that 27 could only be in its right subtree, and then discovered that 25's right subtree was empty. At that point, we can be sure that 27 isn't anywhere in the tree, even though we've only looked at a few of the nodes.

In principle, lookups in binary search trees really are that simple. Start at the root, and proceed downward to the left or right, following one path from the root toward a leaf. If you find what you're looking for at any point, you're done; if not, continue until you either find it or you're led to an empty subtree.

As always, though, we're concerned not only with how the algorithm works, but also with how well it works, so let's do some analysis.

Asymptotic analysis of lookup

From our understanding of the lookup algorithm, it seems clear that the amount of time spent will be a function of how far we have to go. We can compare each key to the key we're searching for in a constant amount of time, which will lead us either to being finished or to take a step downward to the left or the right, always along a single path in the binary search tree. For a binary search tree of height h, we would say that this takes O(h) time, because we might have to follow the longest path in the tree — the length of which is, by definition, the tree's height — and because we might not have to get all the way to a leaf (or follow the path that's the longest).

But a key issue to consider is how the height of the tree, h, relates to the number of nodes in the tree, which we'll call n. This is the thing we'll be most interested in knowing — it's certainly true that more nodes will tend to make searches take longer, but by how much? To answer that, we'll have to consider the shapes that binary search trees can take.

Imagine that we have a binary search tree containing the keys 1, 2, 3, 4, 5, 6, and 7. What shape(s) might it have? There are many possibilities, but there are two extremes. One of those extremes looks like this:

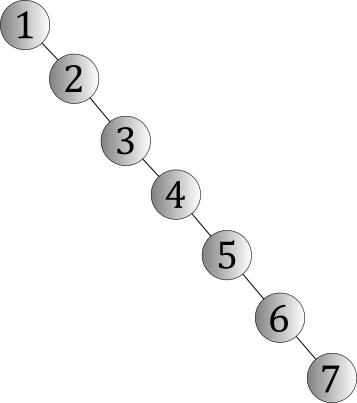
This shape is known as a degenerate tree, so named because this is the worst shape you can be faced with. A degenerate tree is one that contains n nodes and has a height of n − 1. The reason why this shape is so bad is because a lookup would essentially be a linear-time search, because you might have to visit every node. A lookup, given this shape, would take O(n) time, which is no better than unordered linear data structures like arrays or linked lists.

By way of contrast, we might also have the opposite extreme:

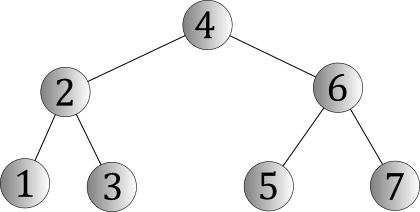
This shape is known as a perfect binary tree, so named because it's as good as it gets. A perfect binary tree with h levels is one in which every level is "full" (i.e., every node that could possibly be on that level will actually be on that level). Thought differently, a perfect binary tree could be defined this way:

A perfect binary tree of height h is a binary tree with the following properties.

• If h = 0, then its left and right subtrees are empty.
• Otherwise, h > 0 and its left and right subtrees are both perfect binary trees of height h - 1.

Our intuition should immediately tell us that this tree's shape is better than that of a degenerate tree, because it's now possible to perform even an unsuccessful lookup without visiting every node; however, the question is "How much better is it?" To understand that, we'll need to know how its height relates to the number of nodes it has. There are a couple of mathematical facts that help:

• A perfect binary tree has 2^k nodes on level k. (So, for example, there will be 2⁰ = 1 nodes on level 0, 2¹ = 2 nodes on level 1, and so on.) This can be proven by induction on k.
• A perfect binary tree of height h has 2^h+1 − 1 nodes. This can be proven by induction on h, with the previous fact being a handy one to use in that proof.

We'll skip the two proofs by induction for now, but the latter of the two facts, in particular, leads to a useful conclusion. If the height of the tree is h and the number of nodes is n, we have:

                n = 2h+1 - 1

Some algebra lets us solve for h instead of n, which will tell us the height of a perfect binary tree with n nodes:

            n + 1 = 2h+1
       log2(n + 1) = h + 1       see interlude on logarithms below
   log2(n + 1) - 1 = h

So, generally, we see that the height of a perfect binary tree with n nodes is Θ(log n). A lookup in a binary search tree with this shape would take O(log n) time.

Interlude: Logarithms in asymptotic notation

You've likely seen before that mathematics defines a logarithm as the inverse of exponentiation, which is what allows us to solve the equation above for h. When we use them in asymptotic notations, you'll notice that we don't generally write a base; we're apt to simply write Θ(log n), rather than something more specific like Θ(log₂n) or Θ(log₁₀n). The reason follows from the formula that is used to convert between logarithms of different bases; the ratio, ultimately, is a constant. The formula for that ratio is:

logan / logbn = logab

So, for example, the ratio of log₂n to log₁₆n is log₂16 = 4, a constant. When we use logarithms in asymptotic notations, then, we need not write a base, because the difference between any two bases is simply a constant factor; constant factors are considered irrelevant in asymptotic notations, so there's no reason to write the base.

Another interlude: How much better is logarithmic than linear?

While there are many shapes a binary search tree might take, we've seen that the two extremes are "degenerate" and "perfect," and that the performance distinction between them is that lookups will take O(n) or O(log n) time, depending on the shape. Is this difference significant? How much better is logarithmic than linear? The answer is much, much better, indeed!

To understand why, consider some values of n and log₂n:

log2n	n
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1,024
11	2,048
12	4,096
13	8,192
14	16,384
15	32,768
16	65,536
17	131,072
18	262,144
19	524,288
20	1,048,576
21	2,097,152
22	4,194,304

The first column would represent the height of a particular perfect binary tree. The second column would represent (roughly) the number of nodes you could store in that tree. So, for example, in a perfect binary tree with 1,000,000 nodes, we would have to visit approximately 20 of them to perform one lookup. With 1,000,000,000 nodes, that number would only increase to 30. The moral of this story is that logarithms grow very, very slowly as n grows, and increasingly slowly the bigger n gets. Logarithmic time, generally, is very good news.

Traversing a binary search tree

We've seen previously that there are, broadly speaking, two kinds of tree traversals: breadth-first and depth-first, and that depth-first traversals come in two categories: preorder and postorder, distinguished by when the visit step is done — preorder traversals visit before traversing subtrees, while postorder traversals visit afterward.

Binary search trees offer one more interesting variant called an inorder traversal, which is another kind of depth-first traversal that can visit all of the keys in a binary search tree is ascending order (i.e., smallest to largest). It does this by using the data-ordering property of binary search trees to its advantage:

• All keys in the left subtree of a node will be smaller than whatever key is in that node.
• The key in that node will be smaller than all of the keys in the right subtree.

The trick, then, is to simply visit the keys in that precise order:

inorder(Tree t):
    if t is not empty:
        inorder(left subtree of t)
        visit(key in root of t)
        inorder(right subtree of t)

With the same algorithm applied recursively, we'll make the same decision at every level of the tree, visiting keys in the left subtree of a node before the key in that node, and the key in that node before visiting keys in its right subtree. This will naturally visit the keys in ascending order, from smallest to largest.

Inserting keys into a binary search tree

Of course, binary search trees don't just fall out of the sky, magically organized the way we've seen. You have to be able to build them, by inserting one key at a time, which means we need an algorithm that lets us insert a key. Given a binary search tree T, our insertion algorithm would modify T so that it has one more node than it did before and the additional key desired. And, notably, the result will still have to be a binary search tree, so we can't do anything that violates the data-ordering property — and we'll need to be sure we don't insert a key that's already present, since the keys must be unique.

Unlike linked lists, insertion into a binary search tree is a trickier problem, because changes in one part of the tree can invalidate other parts of it. For example, suppose we wanted to insert the key 60 into our first example binary search tree:

To do that, one problem we'll need to solve is being sure that 60 is not already in the binary search tree. The simplest way to do that is to do a lookup, using the same algorithm we discussed previously:

• Compare 60 to the key in the root, 30. 60 is larger, so we'll proceed to the right.
• Compare 60 to the key in 30's right child, 55. 60 is larger, so we'll again proceed to the right.
• Compare 60 to the key in 55's right child, 70. 60 is smaller, so we'll now proceed to the left.

At this point, we've reached a point where we can't go any farther; 70 has no left child. This means we know two useful things:

• The key 60 is not in the binary search tree.
• The key 60 could reasonably fit into the binary search tree as the left child of 70.

So, we'll create a new node, make it the left child of 70, and place our key 60 into it.

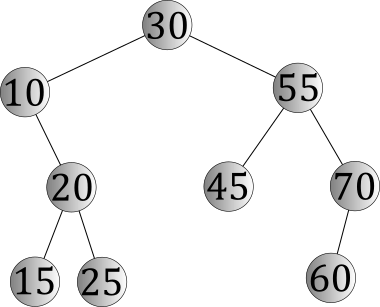
In general, a leaf position is a great place to insert a node into a binary search tree, because it can't cause problems with the nodes above it; as long as the new key "fits" in the leaf position we select, no other keys will be misplaced. By way of contrast, if we tried to insert nodes higher up in the tree, such as making 60 the new root, we would have a lot of work to do in ensuring that we placed the correct nodes into 60's left and right subtrees. And since we have to search for 60, anyway, we'll naturally find the correct leaf position automatically. What's not to like?

Asymptotic analysis of insertion

The asymptotic analysis of insertion is actually quite simple. Fundamentally, it's the same operation as lookup, with the only difference being a constant amount of work — creating a new node and linking it into the tree — done at the end. So, insertion will take O(n) time in a degenerate tree or Θ(log n) time in a perfect binary tree; generally, the smaller the tree's height, the better off we'll be. (The reason that insertion would take Θ(log n) time, rather than O(log n) time, is that we know for sure the insertion would happen at the bottom level of the tree in the case where the tree's shape was perfect.)

Removing a key from a binary search tree

Removing a key from a binary search tree turns out to be somewhat more complicated than the other operations. Lookups are simple because they rely only on the data-ordering property of a binary search tree. Insertions are also relatively straightforward, because we can always insert our new node in a convenient place — a leaf position — where we don't otherwise damage the ordering of the keys already in the tree. But removals don't offer us that option: If we want to remove a key from the tree, we have to deal with it wherever it is, which may or may not be in a convenient place. However, there is one important observation that helps:

When we remove a key from a binary search tree t, the result is a binary search tree t ' with one fewer node than t and the appropriate key missing.

Wording things carefully, we see that the ultimate goal is removing one node and one key. But we don't have to remove the node that currently contains the key we want to remove; if it's in an inconvenient place, we can instead move it somewhere more convenient.

The algorithm involves two steps:

• Perform a lookup, finding the node containing the key we want to remove. (If we don't find it, we're done.)
• Depending on how many children the node has, we'll do different things.

There are three possibilities. Let's consider the effect of removing keys from our most recent binary search tree:

• If we wanted to remove the key 25, it's actually quite simple, because 25 is a node that has no children. We would simply make 20's right subtree be empty (e.g., by pointing a pointer to null) and we would be done; everything else will still be a binary search tree.
• If we wanted to remove the key 70, things are a little more complex, because it has one child, and we have to make sure the orphaned child is placed back into the binary search tree in an appropriate place. An observation helps: All of the keys in 70's left subtree are smaller than 70 but larger than 55 (by definition), which means we could simply make 60 into the right child of 55. In other words, we can remove nodes with one child by simply "pointing around" them. (Note, too, that this would have worked even if 60 had children.)
• If we wanted to remove the key 55, then it gets a bit more complicated than that, because 55 has two children, so we'll have two orphaned children to move around. But there's no law that says we have to remove the node currently containing 55; we just have to remove a node and remove the key 55, with the remaining nodes containing all keys except 55 and being organized as a binary search. This leads to an interesting approach:
  • Find the maximum key in the left subtree of 55 or the minimum key in the right subtree of 55. In practice, it makes little difference which of these you do; either one has the property that you've found a key in one of 55's subtrees that is about as close to 55 as you can get.
  • Swap the key you found with the key 55. So, for example, if we found the minimum key in the right subtree of 55, that key would be 60, so we would swap the keys 55 and 60.
  • The key 55 is now misplaced — it's in 60's right subtree! — but that's fine, because we're going to remove it. And, luckily, it is guaranteed to be in a node that has either zero or one child. Why? Because if the node had two children, 60 wouldn't have been the minimum key in the right subtree; keys in 60's left subtree would have been smaller! So we just remove 55 using one of the simpler cases (zero children or one child) above.

Conceptually, this boils down to the following idea: If the key you want to remove is in an inconvenient place, move it to a convenient place so it becomes easier to remove, though we have to do that a little bit carefully, so we don't disrupt the ordering of other keys in the tree.

Asymptotic analysis of removal

The asymptotic analysis of removal is only slightly more complex than insertion. Fundamentally, it starts with a lookup. After that, it's possible that we'll have to search even further down the tree, looking for the largest or smallest key in some subtree. In total, though, we're only going to follow one path in the tree, and then change a constant number of pointers in the tree to remove the node. So, just like lookup and insertion, removal will take O(n) time in a degenerate tree or O(log n) time in a perfect binary tree; generally, the smaller the tree's height, the better off we'll be.