An old puzzle asks for a partition of the square into triangles in which all angles are strictly acute. This can be solved with eight triangles:
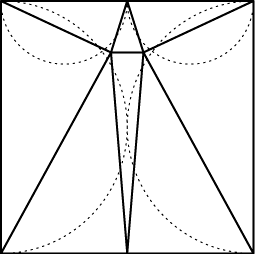
The dashed circles above represent "forbidden regions" in which one of the angles would be obtuse. As Lindgren and Cassidy and Lord showed, eight triangles is best possible, and there exist alternate solutions with any even number of triangles larger than eight.
Recently, John Tromp added a new twist to the problem by asking on sci.math how to make the angles as acute as possible. For the eight-triangle solution, he found a placement of the vertices in which the maximum angle is only about 85 degrees, and asked if more triangles would achieve even better angles.
My own involvement with the problem began several years earlier, with my paper "Provably good mesh generation". One of the ideas in that paper was to define certain "tiles" that could be placed on the squares of a quadtree, to form acute-angled triangulations.
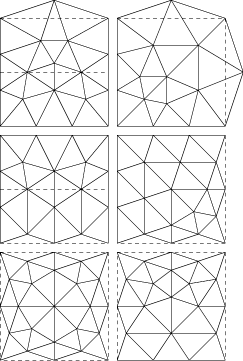

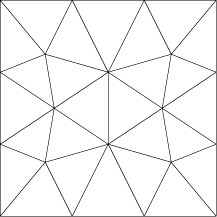
The dashed lines mark the boundaries of the quadtree squares, and indicate that certain half-tiles can be recombined to form three more tiles, including one in which a square is divided into 26 triangles, all having angles of at most 80 degrees. A larger image of the same square tile is shown below. The example triangulation above (which has now become a standard test input in the sparse matrix algorithm community) uses all nine tile types, and also includes several other triangulated squares with larger numbers of triangles.
Later, I and others showed that any polygon could be triangulated with non-obtuse triangles, and that in fact only O(n) non-obtuse triangles suffice to triangulate an n-sided polygon. However some polygons might require right angles or angles very close to 90 degrees.
Returning to Tromp's question on achieving better angles, a result of Gerver implied that the square could be partitioned into 72-degree triangles, not necessarily meeting edge-to-edge. Could this 72-degree bound be achieved by a triangulation in which all triangles met edge to edge? One can't do better than 72 degrees because (by some manipulations with Euler's formula) any triangulated square has (1) a vertex along a square edge where only two triangles meet, (2) a square corner covered by only one triangle, or (3) an interior vertex where at most five triangles meet. Cases (1) and (2) give at best 90 degrees, and case (3) gives at best 72.
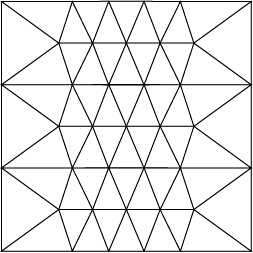
My first solution involved partitioning the square into three rectangles, each triangulated with 20 triangles, for a total of 60 triangles. The ends of each rectangle are covered with one 54-54-72 triangle and two 36-72-72 triangles, and the middle is filled with smaller triangles of varying shapes. There is some "stretch" possible in the middle of the triangulation, so a similar solution can be used to find 72-degree triangulations of any rectangle.
However, this is not best! A fourteen triangle solution is possible.
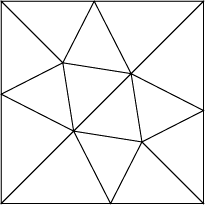
To construct this triangulation, place as guides two congruent regular pentagons, meeting at a face, diagonally in the square (as large as possible, so that four of their corners touch the square's sides). Use as triangulation vertices these four points on the square's sides, the two centers of the pentagons (on one diagonal of the square), and the two points on the other diagonal where the pentagons share a corner. The triangulation has six 54-54-72 triangles (connecting each pentagon center to three pentagon edges), and eight 45-63-72 triangles (two at each corner of the square).
Is fourteen the minimum number of triangles in a 72-degree triangulation of the square?
From the Geometry Junkyard,
computational
and recreational geometry.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Last update: .