Lattice Theory and Geometry of Numbers
Informally, a lattice is an infinite arrangement of points
spaced with sufficient regularity that one can shift any point
onto any other point by some symmetry of the
arrangement. More formally, a lattice can be defined as a discrete
subgroup of a finite-dimensional vector space (the subgroup is
often required not to lie within any subspace of the vector space, which can
be expressed formally by saying that the quotient of the space by the
lattice is compact).
The simplest and most
commonly-studied example of
a lattice (the "integer grid") is formed by the points all Cartesian
coordinates of which are integers.
Other types of lattices arise in crystallography and in
sphere packing, where they are
used to describe the locations of atoms or spheres.
Lattices are also particularly important in the theory of periodic tilings, since they describe the set of
translational symmetries of a tiling.
- Catalogue of lattices, N. J. A. Sloane, AT&T Labs Research.
See also Sloane's sphere-packing and lattice theory publications.
- Connect the dots.
Ed Pegg asks how many sides are needed in a (self-crossing) polygon,
that passes through every point of an n*n grid.
I added a similar puzzle with circular arcs.
- Crystallographic
topology. C. Johnson and M. Burnett of Oak Ridge National Lab use
topological methods to understand and classify the symmetries of the
lattice structures formed by crystals. (Somewhat technical.)
- Equilateral
triangles. Dan Asimov asks how large a triangle will fit into a
square torus; equivalently, the densest packing of equilateral triangles
in the pattern of a square lattice.
There is only one parameter to optimize, the angle of the triangle to
the lattice vectors; my answer
is that the densest packing occurs when
this angle is 15 or 45 degrees, shown below.
(If the lattice doesn't have to be square, it is possible to get density
2/3; apparently this was long known, e.g. see Fáry,
Bull. Soc. Math. France 78 (1950) 152.)
Asimov also asks for the smallest triangle that will always cover at least
one point of the integer lattice, or equivalently a triangle
such that no matter at what angle you place copies of it on an integer lattice,
they always cover the plane; my guess is that the worst angle is parallel
and 30 degrees to the lattice, giving a triangle with 2-unit sides
and contradicting an earlier answer to Asimov's question.
- Grid subgraphs.
Jan Kristian Haugland looks for sets of lattice points that induce
graphs with high degree but no short cycles.
- Mike Kolountzakis' publications include several recent papers on lattice tiling.
- Lattice pentagons.
The vertices of a regular pentagon are not the subset of any lattice.
- The
no-three-in-line problem.
How many points can be placed in an n*n grid with no three
on a common line? The solution is known to be between 1.5n and
2n. Achim Flammenkamp discusses some new computational results
including bounds on the number of symmetric solutions.
- Polyominoes, figures formed from subsets
of the square lattice tiling of the plane. Interesting problems
associated with these shapes include finding all of them, determining
which ones tile the plane, and dissecting rectangles or other shapes
into sets of them. Also includes related
material on polyiamonds, polyhexes, and animals.
- Russian math olympiad problem on lattice
points.
Proof that, for any five lattice points in convex position,
another lattice point is on or inside
the inner pentagon of the five-point star they form.
- Spiral tilings.
These similarity tilings are formed by applying the exponential function
to a lattice in the complex number plane.
- Triangulations with many different areas.
Eddie Grove asks for a function t(n) such that any n-vertex convex polygon
has a triangulation with at least t(n) distinct triangle areas,
and also discusses a special case in which the vertices are points in a
lattice.
- Untitled,
Forbes Gallery, 1987, Ken Goldberg.
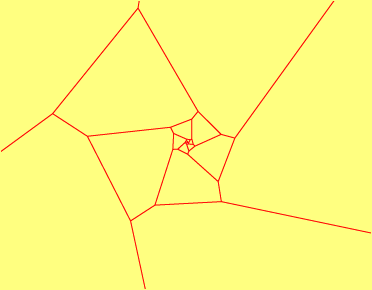
- Voronoi diagrams of lattices.
Greg Kuperberg
discusses an algorithm for constructing the Voronoi cells in a planar
lattice of points. This problem is closely related to some important
number theory: Euclid's algorithm for integer GCD's, continued
fractions, and good approximations of real numbers by rationals.
Higher-dimensional generalizations (in which the Voronoi cells form
zonotopes) are much harder -- one can find a basis of
short vectors using the well-known LLL algorithm, but this doesn't
necessarily find
the vectors corresponding to Voronoi adjacencies. (In fact, according
to Senechal's Quasicrystals and Geometry, although the set
of Voronoi adjacencies of any lattice generates the lattice, it's not
known whether this set always contains a basis.)
From the Geometry Junkyard,
computational
and recreational geometry pointers.
Send email if you
know of an appropriate page not listed here.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Semi-automatically
filtered
from a common source file.