Pentagonal Geometry and the Golden Ratio
This page includes geometric problems defined on regular pentagons,
involving pentagonal angles,
or based on the golden ratio (the ratio of diagonal to
side length in a regular pentagon).
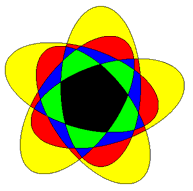
- A
Brunnian link. Cutting any one of five links allows the remaining
four to be disconnected from each other, so this is in some sense a
generalization of the Borromean rings. However since each pair of links
crosses four times, it can't be drawn with circles.
- Constructing a regular pentagon inscribed in a circle, by straightedge and compass.
Scott Brodie.
- Cut-the-knot logo.
With a proof of the origami-folklore that this folded-flat overhand
knot forms a regular pentagon.
- The downstairs half bath.
Bob Jenkins decorated his bathroom with ceramic and painted pentagonal tiles.
- Equilateral
pentagons. Jorge Luis Mireles Jasso investigates these polygons
and dissects various polyominos into them.
- Equilateral
pentagons that tile the plane, Livio Zucca.
- The golden ratio in an equilateral triangle.
If one inscribes a circle in an ideal hyperbolic triangle,
its points of tangency form an equilateral triangle
with side length 4 ln phi!
One can then place horocycles centered on the ideal triangle's vertices
and tangent to each side of the inner equilateral triangle.
From the Cabri geometry site. (In French.)
- The
golden section and geometry. Somehow leading to questions like how
many stars there are on the US flag.
- Golden rectangles, Curtis McMullen.
- A
golden sales pitch. Julie Rehmeyer dissects the myth of the golden
ratio in classical art and describes some new uses for it in commerce.
- The golden
section and Euclid's construction of the dodecahedron, and
more
on the dodecahedron and icosahedron,
H. Serras, Ghent.
- Golden
spiral flash animation, Christian Stadler.
- How many
points can one find in three-dimensional space so that all triangles
are equilateral or isosceles?
One eight-point solution is formed by placing three points
on the axis of a regular pentagon.
This problem seems related to the fact that
any planar point set forms O(n7/3)
isosceles triangles; in three dimensions, Theta(n3) are possible
(by generalizing the pentagon solution above). From Stan Wagon's
PotW archive.
- How to construct a golden rectangle, K. Wiedman.
- Isotiles,
workbook on the shapes that can be formed by combining isosceles
triangles with side lengths in the golden ratio.
- Jiang Zhe-Ming's
geometry challenge. A pretty problem involving cocircularity of five
points defined by circles around a pentagram.
- Largest
5-gon in a square, or more interestingly smallest equilateral
pentagon inscribed in a square.
Posting to sci.math by Rainer Rosenthal.
- Lattice pentagons.
The vertices of a regular pentagon are not the subset of any lattice.
- Miquel's
pentagram theorem on circles associated with a pentagon.
With annoying music.
- Museum of
harmony and golden section.
- Number patterns,
curves, and topology, J. Britton.
Includes sections on the golden ratio, conics, Moiré patterns,
Reuleaux triangles, spirograph curves, fractals, and flexagons.
- Parallel pentagons.
Thomas Feng defines these as pentagons in which each diagonal
is parallel to its opposite side, and asks for a clean construction
of a parallel pentagon through three given points.
(He is aware of the obvious reduction via affine transformation to the
construction of regular pentagons, but finds that non-elegant.)
- Penrose
mandala and five-way Borromean rings.
- Penrose tilings.
This five-fold-symmetric tiling by rhombs or kites and darts
is probably the most well known aperiodic tiling.
- Perplexing
pentagons, Doris Schattschneider, from the Discovering Geometry
Newsletter.
A brief introduction to the problem of tiling the plane by pentagons.
- Pentagon
packing on a circle and on a sphere,
T. Tamai.
- Pentagonal
Tessellations. John Savard experiments with substitution systems to
produce tilings resembling Kepler's.
- Pentagons that tile the plane, Bob Jenkins.
See also
Ed Pegg's page on
pentagon tiles.
- The
pentagram and the golden ratio. Thomas Green, Contra Costa College.
- Russian math olympiad problem on lattice
points.
Proof that, for any five lattice points in convex position,
another lattice point is on or inside
the inner pentagon of the five-point star they form.
- A Venn diagram
made from five congruent ellipses. From F. Ruskey's Combinatorial
Object Server.
- Wonders of Ancient Greek Mathematics, T. Reluga.
This term paper for a course on Greek science includes sections
on the three classical problems, the Pythagorean theorem, the golden
ratio, and the Archimedean spiral.
From the Geometry Junkyard,
computational
and recreational geometry pointers.
Send email if you
know of an appropriate page not listed here.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Semi-automatically
filtered
from a common source file.