Circles and Spheres
- Arc
length surprise. The sum of the areas of the regions between a
circular arc and the x-axis, and between the arc and the y-axis,
does not depend on the position of the arc!
From Mudd Math Fun Facts.
- The Atomium, structure formed
for Expo 1958 in the form of nine spheres, representing an iron
crystal. The world's largest cube?
- Borromean rings don't exist.
Geoff Mess relates a proof that
the Borromean ring configuration
(in which three loops are tangled together but no pair is linked)
can not be formed out of circles.
Dan Asimov discusses some related higher dimensional questions.
Matthew
Cook conjectures the converse.
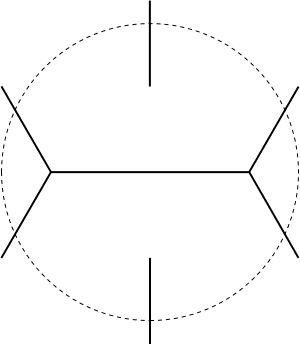
- Building a better beam detector.
This is a set that intersects all lines through the unit disk.
The construction below achieves
total length approximately 5.1547, but better bounds were previously known.
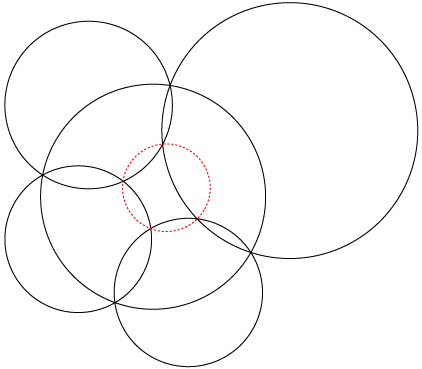
- Circle fractal
based on repeated placement of two equal tangent circles within each
circle of the figure.
One could also get something like this by inversion, starting with three
mutually tangent circles, but then the circles at each level of the
recursion wouldn't all stay the same size as each other.
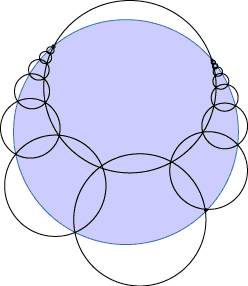
- Circular
coverage constants. How big must N equal disks be in order to
completely cover the unit disk? What about disks with sizes in
geometric progression? From MathSoft's favorite constants pages.
- Circular quadrilaterals.
Bill Taylor notes that if one connects the opposite midpoints
of a partition of the circle into four chords, the two line segments
you get are at right angles. Geoff Bailey supplies an elegant proof.
- Circumcenters of triangles.
Joe O'Rourke, Dave Watson, and William Flis
compare formulas for computing
the coordinates of a circle's center from three boundary points,
and higher dimensional generalizations.
- Circumference/perimeter
of an ellipse: formula(s). Interesting and detailed survey of
formulas giving accurate approximations to this value, which can not be
expressed exactly as a closed form formula.
- Conceptual proof that
inversion sends circles to circles, G. Kuperberg.
- Delaunay and regular triangulations.
Lecture by Herbert Edelsbrunner, transcribed by Pedro Ramos and Saugata
Basu. The regular triangulation has been popularized by Herbert as the
appropriate generalization of the Delaunay triangulation to collections
of disks.
- Escher
sphere construction kit.
- Filling space with unit circles. Daniel
Asimov asks what fraction of 3-dimensional space can be filled by a
collection of disjoint unit circles. (It may not be obvious that this
fraction is nonzero, but a standard construction allows one to construct
a solid torus out of circles, and one can then pack tori to fill space,
leaving some uncovered gaps between the tori.) The geometry center has
information in several places on this problem, the best being an
article
describing a way of filling space by unit circles (discontinuously).
- Five circle theorem.
Karl Rubin and Noam Elkies asked for a proof that a certain construction
leads to five cocircular points. This result was subsequently discovered
by Allan Adler and Gerald Edgar to be essentially the same as a theorem
proven in 1939 by F. Bath.
- Fractal patterns formed by repeated inversion of circles:
Indra's Pearls
Inversion graphics gallery, Xah Lee.
Inversive circles, W. Gilbert, Waterloo.
- Frequently asked questions about spheres. From Dave Rusin's known math pages.
- Hopf fibration.
R. Kreminski,
the U.
Sheffield maths dept., and
MathWorld
explain and animate the partition of a 3-sphere
into circles.
- The HyperSphere, from an Artistic point of View,
Rebecca Frankel.
- Hyperspheres. Eric Weisstein calculates volumes and surface areas of hyperspheres, which curiously reach a maximum for dimensions around 5.257 and 7.257 respectively.
- Inversive geometry. Geometric transformations of circles, animated with CabriJava.
- Jiang Zhe-Ming's
geometry challenge. A pretty problem involving cocircularity of five
points defined by circles around a pentagram.
- The
Kneser-Poulsen Conjecture.
Bezdek and Connelly solve an old problem about pushing disks together.
- Mathematical imagery by Jos Leys.
Knots, Escher tilings, spirals, fractals, circle inversions, hyperbolic
tilings, Penrose tilings, and more.
- Minimax elastic bending energy of sphere eversions.
Rob Kusner, U. Mass. Amherst.
- Miquel's
pentagram theorem on circles associated with a pentagon.
With annoying music.
- Miquel's six
circles in 3d.
Reinterpreting a statement about intersecting circles to be about
inscribed cuboids.
- Monge's
theorem and Desargues' theorem, identified.
Thomas Banchoff relates these two results,
on colinearity of intersections of external tangents to disjoint circles,
and of intersections of sides of perspective triangles, respectively.
He also describes generalizations to higher dimensional spheres.
- The Optiverse.
An amazing 6-minute video on how to turn spheres inside out.
- Platonic spheres.
Java animation, with a discussion of platonic solid classification,
Euler's formula, and sphere symmetries.
- Poncelet's
porism, the theorem that if a polygon is simultaneously
inscribed in one circle and circumscribed in another, then there exists
an infinite family of such polygons, one touching each point of each
circle. From the secret blogging seminar.
- Pushing
disks together. If unit disks move so their pairwise distances all
decrease, does the area of their union also decrease?
- Random spherical arc crossings.
Bill Taylor and Tal Kubo prove that if one takes two random geodesics
on the sphere, the probability that they cross is 1/8.
This seems closely related a famous problem on the probability
of choosing a convex quadrilateral from a planar distribution.
The minimum (over all possible distributions) of this probability
also turns out to solve a seemingly unrelated combinatorial
geometry problem, on the minimum
number of crossings possible in a drawing of the complete graph with
straight-line edges:
see also "The
rectilinear crossing number of a complete graph
and Sylvester's four point problem of geometric probability",
E. Scheinerman and H. Wilf, Amer. Math. Monthly 101 (1994) 939-943,
rectilinear
crossing constant, S. Finch, MathSoft, and
Calluna's pit,
Douglas Reay.
- The
reflection of light rays in a cup of coffee or
the curves obtained with b^n mod p, S. Plouffe, Simon Fraser U.
(Warning: large animated gif. You may prefer the more wordy explanation at
Plouffe's other page on the same subject.)
- Vittoria Rezzonico's
Java applets. Hypercube and polyhedron visualization, and circle
inversion patterns. Requires both Java and JavaScript.
- Sausage
Conjecture. L. Fejes Tóth conjectured that, to minimize the volume of the convex hull of
hyperspheres in five or more dimensions, one should line them up in a row.
This has recently been solved for very high dimensions
(d > 42) by Betke and Henk
(see also Betke et al., J. Reine Angew. Math. 453 (1994) 165-191
and the
MathWorld
Sausage Conjecture Page).
- Seven
circle theorem, an applet illustrating the fact that if six circles
are tangent to and completely surrounding a seventh circle, then
connecting opposite points of tangency in pairs forms three lines that
meet in a single point, by Michael Borcherds.
Other applets by Borcherds
include Poncelet's
porism, a similar porism with an ellipse and a parabola and with two ellipses,
and more generally with two conics of variable type.
- Sierpinski carpet on the sphere.
From Curtis McMullen's
math gallery.
- Sliced ball.
Ray-traced image created to help
describe recent algorithms
for removing slivers from tetrahedral meshes.
- Soccer
ball pictures,
spherical patterns generated by reflections that form rational angles to each
other.
- Sphere packing and kissing numbers.
How should one arrange circles or spheres
so that they fill space as densely as possible?
What is the maximum number of spheres that can simultanously touch
another sphere?
- Tangencies.
Animated compass and straightedge constructions of
various patterns of tangent circles.
- Tangencies
of circles and spheres. E. F. Dearing provides formulae for the
radii of Apollonian circles, and analogous three-dimensional problems.
- Tetrahedrons and spheres.
Given an arbitrary tetrahedron, is there a sphere tangent to each of its edges?
Jerzy Bednarczuk, Warsaw U.
- Morwen Thistlethwait,
sphere packing, computational topology, symmetric knots,
and giant ray-traced floating letters.
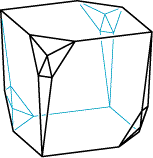
- An uninscribable 4-regular polyhedron.
This shape can not be drawn with all its vertices on a single sphere.
- Visualizing the hypersphere via 3d slices, and
other
four-dimensional thoughts by Jeff Fuquay.
- WWW spirograph.
Fill in a form to specify radii,
and generate pictures by rolling one circle around another.
For more pictures of cycloids, nephroids, trochoids,
and related spirograph shapes, see David Joyce's
Little Gallery of Roulettes.
Anu Garg
has implemented spirographs in Java.
- yukiToy. Shockwave plugin software for pushing around a few reddish spheres in
your browser window. But what exactly is the point?
(They're spheres, they don't have one, I guess.)
From the Geometry Junkyard,
computational
and recreational geometry pointers.
Send email if you
know of an appropriate page not listed here.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Semi-automatically
filtered
from a common source file.