Tiling

• Aperiodic colored tilings, F. Gähler. Also available in postscript.

• An aperiodic set of Wang cubes, J. UCS 1:10 (1995). Culik and Kari describe how to increase the dimension of sets of aperiodic tilings, turning a 13-square set of tiles into a 21-cube set.

• Aperiodic space-filling tiles: John Conway describes a way of glueing two prisms together to form a shape that tiles space only aperiodically. Ludwig Danzer speaks at NYU on various aperiodic 3d tilings including Conway's biprism.

• Chaotic tiling of two kinds of equilateral pentagon, with 30degree symmetry, Ed Pegg Jr.

• Cognitive Engineering Lab, Java applets for exploring tilings, symmetry, polyhedra, and four-dimensional polytopes.

• Complex regular tesselations on the Euclid plane, Hironori Sakamoto.

• a computational approach to tilings. Daniel Huson investigates the combinatorics of periodic tilings in two and three dimensions, including a classification of the tilings by shapes topologically equivalent to the five Platonic solids.

• Cool math: tessellations

• Andrew Crompton. Grotesque geometry, Tessellations, Lifelike Tilings, Escher style drawings, Dissection Puzzles, Geometrical Graphics, Mathematical Art. Anamorphic Mirrors, Aperiodic tilings, Optical Machines.

• Delta Blocks. Hop David discusses ideas for manufacturing building blocks based on the tetrahedron-octahedron space tiling depicted in Escher's "Flatworms".

• Dérivés de l'hexagone. Art by Jerome Pierre based on modifications to the edges in a hexagonal tiling of the plane.

• Dissection and dissection tiling. This page describes problems of partitioning polygons into pieces that can be rearranged to tile the plane. (With references to publications on dissection.)

  

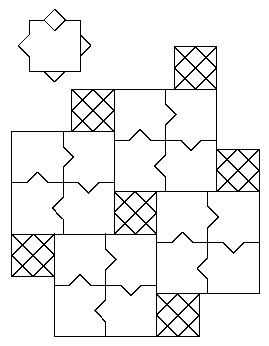
• The downstairs half bath. Bob Jenkins decorated his bathroom with ceramic and painted pentagonal tiles.

• Equilateral pentagons that tile the plane, Livio Zucca.

• The equivalence of two face-centered icosahedral tilings with respect to local derivability, J. Phys. A26 (1993) 1455. J. Roth dissects an aperiodic three-dimensional tiling involving zonohedra into another tiling involving tetrahedra and vice versa.

• Escher-like tilings of interlocking animal and human figures, by various artists.

• Fisher Pavers. A convex heptagon and some squares produce an interesting four-way symmetric tiling system.

• Five space-filling polyhedra. And not the ones you're likely thinking of, either. Guy Inchbald, reproduced from Math. Gazette 80, November 1996.

• The fractal art of Wolter Schraa. Includes some nice reptiles and sphere packings.

• Fractal reptiles and other tilings by IFS attractors, Stewart Hinsley.

• Fractal tilings.

• Fractiles, multicolored magnetic rhombs with angles based on multiples of pi/7.

• Gallery of interactive on-line geometry. The Geometry Center's collection includes programs for generating Penrose tilings, making periodic drawings a la Escher in the Euclidean and hyperbolic planes, playing pinball in negatively curved spaces, viewing 3d objects, exploring the space of angle geometries, and visualizing Riemann surfaces.

• Geometric Arts. Knots, fractals, tesselations, and op art. Formerly Quincy Kim's World of Geometry.

• Ghost diagrams, Paul Harrison's software for finding tilings with Wang-tile-like hexagonal tiles, specified by matching rules on their edges. These systems are Turing-complete, so capable of forming all sorts of complex patterns; the web site shows binary circuitry, fractals, 1d cellular automaton simulation, Feynman diagrams, and more.

• Heesch's problem. How many times can a shape be completely surrounded by copies of itself, without being able to tile the entire plane? W. R. Marshall and C. Mann have recently made significant progress on this problem using shapes formed by indenting and outdenting the edges of polyhexes.

  

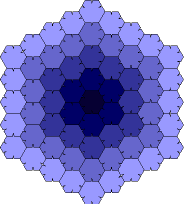
• Infect. Eric Weeks generates interesting colorings of aperiodic tilings.

• Investigating Patterns: Symmetry and Tessellations. Companion site to a middle school text by Jill Britton, with links to many other web sites involving symmetry or tiling.

• Irreptiles. Karl Scherer and Erich Friedman generalize the concept of a reptile (tiling of a shape by smaller copies of itself) to allow the copies to have different scales. See also Karl Scherer's two-part irreptile puzzle.

  

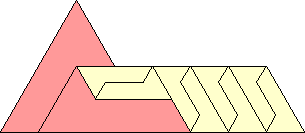
• The isoperimetric problem for pinwheel tilings. In these aperiodic tilings (generated by a substitution system involving similar triangles) vertices are connected by paths almost as good as the Euclidean straight-line distance.

• Jovo Click 'n Construct. Plastic click-together triangular, square, and pentagonal tiles for building models of polyhedra and polygonal tilings. Includes a mathematical model gallery showing examples of shapes constructable from Jovo.

• Kaleidotile software for visualizing tilings of the sphere, Euclidean plane, and hyperbolic plane.

• Keller's cube-tiling conjecture is false in high dimensions, J. Lagarias and P. Shor, Bull. AMS 27 (1992). Constructs a tiling of ten-dimensional space by unit hypercubes no two of which meet face-to-face, contradicting a conjecture of Keller that any tiling included two face-to-face cubes.

• Richard Kenyon's Gallery of tilings by squares and equilateral triangles of varying sizes.

• Mike Kolountzakis' publications include several recent papers on lattice tiling.

• Labyrinth tiling. This aperiodic substitution tiling by equilateral and isosceles triangles forms fractal space-filling labyrinths.

  

• Lenses, rational-angled equilateral hexagons can tile the plane in various interesting patterns. See also Jorge Mireles' nice lens puzzle applet: rotate decagons and stars to get the pieces into the right places.

• Log-spiral tiling, and other radial and spiral tilings, S. Dutch.

• Mathematical origami, Helena Verrill. Includes constructions of a shape with greater perimeter than the original square, tessellations, hyperbolic paraboloids, and more.

• Mitre Tiling. Ed Pegg describes the discovery of the versatile tiling system (with Adrian Fisher and Miroslav Vicher), also discussing many other interesting tilings including a tile that can fill the plane with either five-fold or six-fold symmetry.

• Modularity in art. Slavik Jablan explores connections between art, tiling, knotwork, and other mathematical topics.

• New directions in aperiodic tilings, L. Danzer, Aperiodic '94.

• Non periodic tiling of the plane. Including Penrose tiles, Pinhweel tiling, and more. Paul Bourke.

• Nontrivial convexity. Ed Pegg asks about partitions of convex regions into equal tiles, other than the "trivial" ones in which some rotational or translational symmetry group relates all the tile positions to each other. See also Miroslav Vicher's page on nontrivial convexity

• Origami tessellations and paper mosaics, Alex Bateman.

• Parquet deformations. Craig Kaplan involves continuous spatial transformations of one tiling to another.

• Penrose tilings. This five-fold-symmetric tiling by rhombs or kites and darts is probably the most well known aperiodic tiling.

• Perplexing pentagons, Doris Schattschneider, from the Discovering Geometry Newsletter. A brief introduction to the problem of tiling the plane by pentagons.

• Pentagonal Tessellations. John Savard experiments with substitution systems to produce tilings resembling Kepler's.

• Pentagons that tile the plane, Bob Jenkins. See also Ed Pegg's page on pentagon tiles.

• Perron Number Tiling Systems. Mathematica software for computing fractals that tile the plane from Perron numbers.

• Platonic tesselations of Riemann surfaces, Gerard Westendorp.

• Polygons with angles of different k-gons. Leroy Quet asks whether polygons formed by combining the angles of different regular polygons can tile the plane. The answer turns out to be related to Egyptian fraction decompositions of 1 and 1/2.

• PolyMultiForms. L. Zucca uses pinwheel tilers to dissect an illustration of the Pythagorean theorem into few congruent triangles.

• Polyomino tiling. Joseph Myers classifies the n-ominoes up to n=15 according to how symmetrically they can tile the plane.

• Polyominoes, figures formed from subsets of the square lattice tiling of the plane. Interesting problems associated with these shapes include finding all of them, determining which ones tile the plane, and dissecting rectangles or other shapes into sets of them. Also includes related material on polyiamonds, polyhexes, and animals.

• ProtoZone interactive shockwave museum exhibits for exploring geometric concepts such as symmetry, tiling, and wallpaper groups.

• Publications on quasicrystals and aperiodic tilings, F. Gähler.

• A Puzzling Journey To The Reptiles And Related Animals, and New Mosaics. Books on tiling by Karl Scherer.

• Quaquaversal Tilings and Rotations. John Conway and Charles Radin describe a three-dimensional generalization of the pinwheel tiling, the mathematics of which is messier due to the noncommutativity of three-dimensional rotations.

  Quasicrystals and aperiodic tilings, A. Zerhusen, U. Kentucky. Includes a nice description of how to make 3d aperiodic tiles from zometool pieces.

• Reptile project-of-the-month from the Geometry Forum. Form tilings by dividing polygons into copies of themselves.

• Rhombic spirallohedra, concave rhombus-faced polyhedra that tile space, R. Towle.

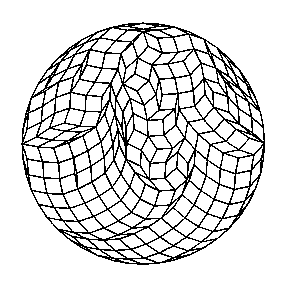
• Rhombic tilings. Abstract of Serge Elnitsky's thesis, "Rhombic tilings of polygons and classes of reduced words in Coxeter groups". He also supplied the picture below of a rhombically tiled 48-gon, available with better color resolution from his website.

  

• Self-affine tiles, J. Lagarias and Y. Wang, DIMACS. Mathematics of a class of generalized reptiles.

• Semi-regular tilings of the plane, K. Mitchell, Hobart and William Smith Colleges.

• Some generalizations of the pinwheel tiling, L. Sadun, U. Texas.

• SpaceBric building blocks and Windows software based on a tiling of 3d space by congruent tetrahedra.

• Spidron, a triangulated double spiral shape tiles the plane and various other surfaces. With photos of related paperfolding experiments.

• Spiral tilings. These similarity tilings are formed by applying the exponential function to a lattice in the complex number plane.

  

• Symmetry, tilings, and polyhedra, S. Dutch.

• Symmetry and Tilings. Charles Radin, Not. AMS, Jan. 1995. See also his Symmetry of Tilings of the Plane, Bull. AMS 29 (1993), which proves that the pinwheel tiling is ergodic and can be generated by matching rules.

• Taprats Java software for generating symmetric Islamic-style star patterns.

• Tesselating locking polyominos, Bob Newman.

• Tessellation links, S. Alejandre.

• Tessellation resources. Compiled for the Geometry Center by D. Schattschneider.

• 3D-Geometrie. T. E. Dorozinski provides a gallery of images of 3d polyhedra, 2d and 3d tilings, and subdivisions of curved surfaces.

• Tilable perspectives. Patrick Snels creates two-dimensional images which tile the plane to form 3d-looking views including some interesting Escher-like warped perspectives. See also his even more Escherian tesselations page.

• Tiling plane & fancy, Steven Edwards, SPSU.

• Tiling the infinite grid with finite clusters. Mario Szegedy describes an algorithm for determining whether a (possibly disconnected) polyomino will tile the plane by translation, in the case where the number of squares in the polyomino is a prime or four.

• Tiling the integers with one prototile. Talk abstract by Ethan Coven on a one-dimensional tiling problem on the boundary between geometry and number theory, with connections to factorization of finite cyclic groups. See also Coven's paper with Aaron Meyerowitz, Tiling the integers with translates of one finite set.

• Tiling problems. Collected at a problem session at Smith College, 1993, by Marjorie Senechal.

• Tiling transformer. Java applet for subdividing tilings (starting from a square or hexagonal tiling) in various different ways.

  

• Tiling dynamical systems. Chris Hillman describes his research on topological spaces in which each point represents a tiling.

• On a tiling scheme by M. C. Escher, D. Davis, Elect. J. Combinatorics.

• Tilings of hyperbolic space.

• Tilings and visual symmetry, Xah Lee.

• Toroidal tile for tessellating three-space, C. Séquin, UC Berkeley.

• Totally Tessellated. Mosaics, tilings, Escher, and beyond.

• Triangle tiling. Geom. Ctr. exhibit at the Science Museum of Minnesota.

• Federation Square. This building in Melbourne uses the pinwheel tiling as a design motif. Thanks to Khalad Karim for identifying it. Photos by Dick Hess, scanned by Ed Pegg Jr. See this Flickr photopool for many more photos.

   

• true_tile mailing list for discussion of Euclidean and non-Euclidean tilings.

• Tysen loves hexagons. And supplies ascii, powerpoint, and png graphics for several styles of hexagonal grid graph paper.

• Unbalanced anisohedral tiling. Joseph Myers and John Berglund find a polyhex that must be placed two different ways in a tiling of a plane, such that one placement occurs twice as often as the other.