How does it do it?
There are two commonly used algorithms: Knuth-Morris-Pratt (KMP) and Boyer-Moore (BM). Both use similar ideas. Both take linear time: O(m + n) where m is the length of the search string, and n is the length of the file. Both only test whether certain characters are equal or unequal, they don't do any complicated arithmetic on characters.
Boyer-Moore is a little faster in practice, but more complicated. Knuth-Morris-Pratt is simpler, so it's the one we'll discuss. The book talks about it in terms of finite state machines which would be fine if you'd taken 162 but you haven't....
It's explicitly algorithmic: we represent the language as the set of those strings accepted by some program. So, once you've found the right machine, you can test whether a given string matches just by running it.
The KMP algorithm works by turning the pattern it's given into a machine, and then running the machine. The hard part of KMP is finding the machine.
We need some restrictions on what we mean by "program". This is where "deterministic & finite" come from.
One way of thinking about it, is in terms of programs without any variables. All such a program can do is look at each incoming character determine what line to go to, and eventually return true or false (depending on whether it thinks the string matches or doesn't).
main()
{
for (;;) {
if (getchar() == EOF) return TRUE;
if (getchar() == EOF) return FALSE;
}
}
Note the lack of variables. To simplify things, we'll rewrite
programs to avoid complicated loops, and instead just use goto statements. (You've probably been taught that gotos
are bad, but this sort of rewriting happens all the time, in fact
every time you run a compiler it has to do this.)
main()
{
even:
if (getchar() == EOF) return TRUE;
else goto odd;
odd:
if (getchar() == EOF) return FALSE;
else goto even;
}
We've chosen labels for the goto statements, to represent what we
know about the string so far (in this problem, whether we've seen
an even or odd number of characters so far). Because there are no
variables, we can only represent knowledge about the input in terms
of where we are in the program. We think of each line in the
program as being a state, representing
some specific fact about the part of the string we've seen so far.
Here the states are "even" and "odd", and represent what we know
about the number of characters seen so far.
Since there are no variables, the only thing a machine can do in a given state (state = what line the prog is on) is to go to different states, depending on what character it sees.
This can be a useful programming style; for instance I am using a program written in close to this style to filter some html files on my web pages. One advantage of this style is that there are few ways the program can be tricked into having unexpected values in its variables (since there are no variables) so it is hard to make such a program crash. But it's a little long and cumbersome, and you wouldn't want to have to compile a separate C program every time you ran "grep".
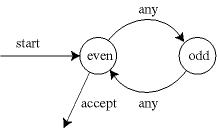
Rather than writing C code, we'll draw pictures with circles and arrows. (These pictures are known as state diagrams.) A circle will represent a state, an arrow with a label will represent that we go to that state if we see that character. (You can think of this as just being a special kind of graph.) We'll also draw an arrow from nowhere to the first state the program starts in, and arrows to nowhere if the program returns true if the string ends at that state. So our program can be represented with the following diagram.

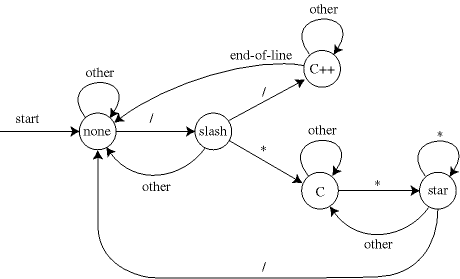
In class I described a more complicated example, that could be used by the C preprocessor (a part of most C compilers) to tell which characters are part of comments and can be removed from the input:
It's easy to turn such a diagram into a program, that simply has one label and one case statement per state.
If we're given such a diagram, and a string, we can easily see whether the corresponding program returns true or false. Simply place a marker (such as a penny) on the initial state, and move it around one state at a time until you run out of characters. Once you run out of characters, see whether the state you're in has an "accept" arrow -- if so, the pattern matches, and if not it doesn't.
In a computer, we obviously don't represent these things with circles and arrows. Instead they can be viewed as just being a special kind of graph, and we can use any of the normal graph representations to store them.
One particularly useful representation is a transition table: we make a table with rows indexed by states, and columns indexed by possible input characters. Then simulating the machine can be done simply by looking up each new step in the table. (You also need to store separately the start and accept states.) For the machine above that tests whether a string has even length, the table might look like this:
any
---
even: odd
odd: even
For the C comment machine, we get a more complicated table:
/ * EOL other
--- --- --- ---
none: slash none none none
slash: C++ C none none
C++: C++ C++ none C++
C: C star C C
star: none star C C
Since a state diagram is just a kind of graph, we can use graph
algorithms to find some information about finite state machines.
For instance we can simplify them by eliminating
unreachable states, or find the shortest path through the
diagram (which corresponds to the shortest string
accepted by that machine).
So we want our states to be partial matches to the pattern. The possible partial matches to "nano" are "", "n", "na", "nan", or (the complete match) "nano" itself. In other words, they're just the prefixes of the string. In general, if the pattern has m characters, we need m+1 states; here m=4 and there are five states.
The start and accept states are obvious: they are just the 0- and m-character prefixes. So the only thing we need to decide is what the transition table should look like. If we've just seen "...nan", and see another character "x", what state should we go to? Clearly, if x is the next character in the match (here "o"), we should go to the next longer prefix (here "nano"). And clearly, once we've seen a complete match, we just stay in that state. But suppose we see a different character, such as "a"? That means that the string so far looks like "...nana". The longest partial match we could be in is just "na". So from state "nan", we should draw an arrow labeled "a" to state "na". Note that "na" is a prefix of "nano" (so it's a state) and a suffix of "nana" (so it's a partial match consistent with what we've just seen).
In general the transition from state+character to state is the longest string that's simultanously a prefix of the original pattern and a suffix of the state+character we've just seen. This is enough to tell us what all the transitions should be. If we're looking for pattern "nano", the transition table would be
n a o other
--- --- --- ---
empty: "n" empty empty empty
"n": "n" "na" empty empty
"na": "nan" empty empty empty
"nan": "n" "na" "nano" empty
"nano": "nano" "nano" "nano" "nano"
For instance the entry in row "nan" and column n says that the
largest string that's simultaneously a prefix of "nano" and a
suffix of "nan"+n="nann" is simply "n". We can also represent this
as a state diagram:
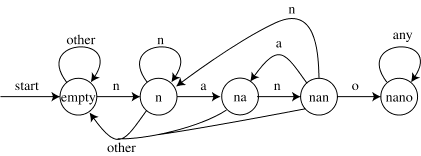
Simulating this on the string "banananona", we get the sequence of states empty, empty, empty, "n", "na", "nan", "na", "nan", "nano", "nano", "nano". Since we end in state "nano", this string contains "nano" in it somewhere. By paying more careful attention to when we first entered state "nano", we can tell exactly where it occurs; it is also possible to modify the machine slightly and find all occurrences of the substring rather than just the first occurrence.
This description is enough to get a string matching algorithm that takes something like O(m^3 + n) time: O(m^3) to build the state table described above, and O(n) to simulate it on the input file. There are two tricky points to the KMP algorithm. First, it uses an alternate representation of the state table which takes only O(m) space (the one above could take O(m^2)). And second, it uses a complicated loop to build the whole thing in O(m) time. We'll see this algorithm next time.
ICS 161 -- Dept.
Information & Computer Science -- UC Irvine
Last update: