

For more descriptions of these and other applications of computational geometry, see my web site "Geometry in Action".
Today's lecture will describe algorithms for two simple geometric problems: determining whether a point is in a polygon, and finding convex hulls. Next quarter I will be offering ICS 164, a class devoted entirely to geometric algorithms, in which I'll describe some more algorithms and applications, for instance the binary space partitions used by Doom.
(0,0), (0,1), (1,1), (1,0)
form a square. The line segments of the polygon connect adjacent
points in the list, together with one additional segment connecting
the first and last point.
Not all sequences of points form a polygon; for instance the points
(0,-1), (0,1), (1,0), (0,-1)
would result in two segments that cross each other. Sometimes we
use the phrase simple polygon to emphasize the requirement
that no two segments cross.
For uncomplicated enough polygons, it's easy to see by eye which parts of the plane are inside and which are outside. But this is not always easy. For instance is the marked point inside the following polygon?

Seemingly even more difficult, we'd like to answer questions like this on a computer, which doesn't have built into it the powerful visual processing system that we have, and can only deal with this sort of problem by translating it to a collection of numbers. The general problem we'd like to solve is, given a point (x,y) (represented by those two numbers) and a polygon P (represented by its sequence of vertices), is (x,y) in P, on the boundary, or outside?
This is a commonly occurring problem, enough so that it is one of the most frequently asked questions on the comp.graphics.algorithms newsgroup. For instance if you want to display a polygon on a computer screen, you need to be able to test whether each pixel of the screen corresponds to a point that's inside or outside the polygon, so you can tell what color to draw it.
Fortunately the problem has a simple and elegant answer. Just draw a ray (portion of a line extending infinitely in one direction) down (or in any other direction) from (x,y):
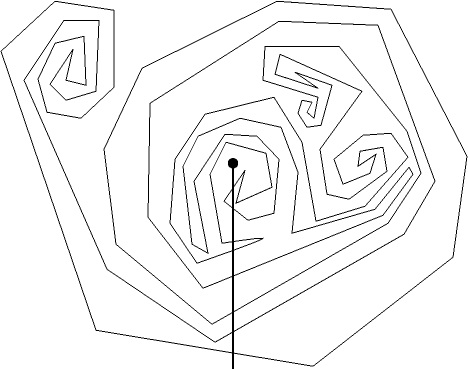
Every time the polygon crosses this ray, it separates a part of the ray that's inside the polygon from a part that's outside. Eventually the ray will get far from the polygon, at which point we know that that part is outside the polygon. We can then work backwards from there, declaring different parts of the ray to be inside or outside alternately at each crossing. Actually, we don't even need to look at what order these crossings occur in; all we really need to know is whether there's an even or odd number of them. In the example shown above, there are eight crossings, so the point is outside the polygon.
We can now write a rough outline of pseudo-code for this problem:
int crossings = 0
for (each line segment of the polygon)
if (ray down from (x,y) crosses segment)
crossings++;
if (crossings is odd)
return (inside);
else return (outside);
As we'll see, we also need to be a little more careful: crossings can also occur at vertices of the polygon, and we haven't checked whether (x,y) sits exactly on the boundary. First let's see how to implement the steps of this pseudo-code.
How do we tell if the ray down from (x,y) crosses the segment between two points (x1,y1) and (x2,y2)? All points of the ray have the same first coordinate x. If this is to be between (x1,y1) and (x2,y2) then x should be between x1 and x2; either (x1<x and x<x2) or (x1>x and x>x2). We can write this more succinctly as (x1-x)(x2-x)<0 but this might actually slower since it involves a high-precision multiplication.
Now suppose x is between x1 and x2. Where is the crossing point? Does it have a smaller second coordinate than y? One definition of the line determined by points (x1,y1) and (x2,y2) is that it consists of all points of the form
(t x1 + (1-t)x2, t y1 + (1-t)y2)
where different values of t give different points on the line. To
find the second coordinate of the crossing, let's use the known
value of the first coordinate to solve for t:
x = t x1 + (1-t)x2
t = (x - x2) / (x1 - x2)
crossing = (x, t y1 + (1-t)y2)
Note that we can also tell if (x,y) is exactly on the line segment
by testing whether y=crossing. Here's a little problem: this
formula might involve a division by zero. But in that case x1=x2 so
x couldn't be between the two. As long as we only compute t when x
is between x1 and x2, we're safe. Let's plug these formulas into
our pseudo-code. We'll let n denote the number of points in the
polygon, and P(i).x and P(i).y denote the coordinates of point (i
mod n).
int crossings = 0
for (int i = 0; i < n; i++)
if ((P(i).x < x && x < P(i+1).x) || (P(i).x > x && x > P(i+1).x))
{
t = (x - P(i+1).x) / (P(i).x - P(i+1).x)
cy = t*P(i).y + (1-t)*P(i+1).y
if (y == cy) return (on boundary)
else if (y > cy) crossings++;
}
if (crossings is odd)
return (inside);
else return (outside);
Finally, what happens if the ray from (x,y) passes exactly through
a vertex of P? Sometimes this should count as a crossing, but
sometimes the ray only "grazes" P and shouldn't count as a
crossing. There are lots of cases to consider, so this may be
confusing. A standard way to cut through this sort of complication
is to perturb the problem: move the points slightly so these
special cases don't happen. For instance, we could move the point
(x,y) just a tiny amount to the right; this won't change whether
it's inside or outside the polygon but will change whether the ray
crosses through any vertices. In fact, we can perform this
perturbation only in our minds, and let it guide us in thinking
about solving the problem, without actually moving any points.
Suppose the ray would cross a vertex before it was perturbed. After
the perturbation, which edges would it cross? Just the ones that go
to the right of the vertex. We can test the two rays out of the
vertex and see which of them go rightwards, and adjust the count
accordingly. Again, we also need to be careful about testing
whether the point is exactly on the boundary of the polygon; the
most complicated case is when this happens on a vertical line
segment.
int crossings = 0
for (int i = 0; i < n; i++)
{
if ((P(i).x < x && x < P(i+1).x) || (P(i).x > x && x > P(i+1).x))
{
t = (x - P(i+1).x) / (P(i).x - P(i+1).x)
cy = t*P(i).y + (1-t)*P(i+1).y
if (y == cy) return (on boundary)
else if (y > cy) crossings++;
}
if ((P(i).x == x && P(i).y <= y) {
if (P(i).y == y) return (on boundary);
if (P(i+1).x == x)
{
if ((P(i).y <= y && y <= P(i+1).y) || (P(i).y >= y && y >= P(i+1).y))
return (on boundary);
} else if (P(i+1).x > x) crossings++;
if (P(i-1).x > x) crossings++;
}
}
if (crossings is odd)
return (inside);
else return (outside);
This is almost completely expanded to compilable code, and it's not
too long, but not easy to read. To understand the ideas behind the
algorithm, I'd stick with the pseudo-code I started with in the
previous section.
Convex polygons are typically much easier to deal with than non-convex ones. As an example, let's see how to simplify the point-in-polygon test.
Let P(i) be the leftmost point of the polygon, and P(j) be the rightmost point. These two points divide the polygon into two parts, the upper chain and the lower chain. Any line or ray crosses the polygon at most twice, and any vertical line or ray crosses each chain at most once.
So a lot of the work of the previous point-in-polygon algorithm is wasted -- we go through each segment checking whether it gives a crossing, but the answer will be yes in at most two cases.
How can we find these two cases more quickly? Binary search. Just search for x in the first coordinates of points in the two chains. If it is in the chain, you have found a crossing through a vertex (and you don't have to be as careful to tell what kind of crossing, either). If x is not the coordinate of a vertex in the chain, the two nearest values to it tell you which segment the ray from (x,y) might cross. So we can test whether a point is in a convex polygon in time O(log n).
It turns out that there are data structures that can test whether a point is in an arbitrary polygon (or which of several polygons it's in) in the same O(log n) time bound. But they're more complicated, so I don't have time to describe them here; I'll talk about them at some point in ICS 164.
I'll describe an algorithm for finding convex hulls known as the Graham scan. The idea is a common one in computational geometry, known as an incremental algorithm: add items one at a time to some structure, maintaining as you do a partial solution for the items added so far. The order in which items are added is often important; the Graham scan adds points in sorted order from left to right (by the values of their first coordinates). So O(n log n) time is needed for an initial sorting stage, or less time if you want to assume e.g. that the points' coordinates are small integers.
The algorithm is easier to describe in terms of the upper and lower chains defined earlier. I'll describe how to compute the upper chain; the lower chain is completely symmetric. Because of the order in which we add points, the first point is always the left end of the upper chain, and the last point is always the right end. The only question is, what happens in the middle?
The figure below shows what happens when we add one new point to the upper chain. We know it should be at the right end, so let's try adding it after the previous rightmost point. However, this might make an indentation at that previous point; if so we remove the indentation from the chain, making it have one less edge. We keep removing indentations one by one until there are none left, at which point we have the new chain.
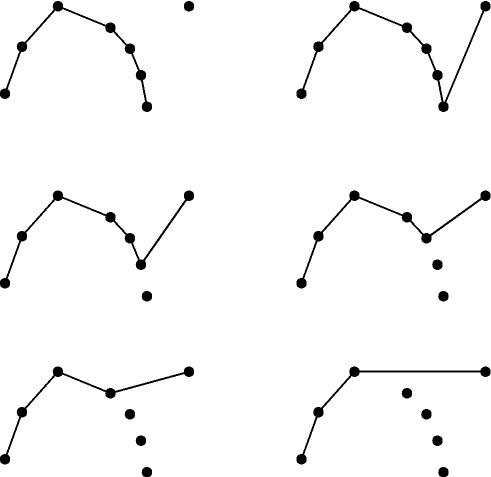
This is easiest to implement if we maintain the chain using a stack data structure. Each new point in the chain corresponds to a push in the stack, and removing an indentation corresponds to a pop. Here is some pseudocode:
stack S = empty
for each point (x,y) in sorted order by x
{
if (x,y) and top two points on S are indented
pop S
push (x,y) onto S
}
The only question is how we test whether three points (x0,y0),
(x1,y1), and (x2,y2) form an indentation. Since we know in this
case the ordering of the x-coordinates of the three points, all we
need to do is test whether the middle point is above or below the
line segment formed by the other two. This is basically the same as
the math I went through to detect crossings for the
point-in-polygon test.
The algorithm goes through O(n) iterations of the outer loop. There is also an inner nested loop, but each iteration of the inner loop removes a point from the stack, and each point can only be removed once, so this happens O(n) times total. Therefore the total time for the convex hull algorithm, after the initial sorting stage, is O(n). The overall algorithm takes time O(n log n) because of the sorting step.
A similar process of shortcutting indentations also works for finding convex hulls of simple polygons. Of course you could just sort the vertices of the polygon and apply Graham scan, but you can instead do the shortcutting process on the polygon itself. It is possible for a shortcut to add a crossing between two edges, but these will always become untangled by later stages of the angles. In this way, one can find convex hulls of simple polygons in linear time, without taking the time for a sorting stage.
ICS 161 -- Dept.
Information & Computer Science -- UC Irvine
Last update: