Antipodes.
Jim Propp asks whether the two farthest apart points,
as measured by surface distance, on a symmetric convex body
must be opposite each other on the body.
Apparently this is open even for rectangular boxes.
Centers of maximum matchings.
Andy Fingerhut asks, given a maximum (not minimum) matching of six
points in the Euclidean plane, whether there is a center point
close to all matched edges (within distance a constant times the length
of the edge). If so, it could be extended to more points via Helly's theorem.
Apparently this is related to communication network design.
I include a response I sent with a proof (of a constant worse than the
one he wanted, but generalizing as well to bipartite matching).
A Counterexample to Borsuk's Conjecture, J. Kahn and G. Kalai,
Bull. AMS 29 (1993). Partitioning certain high-dimensional polytopes
into pieces with smaller diameter requires a number of pieces
exponential in the dimension.
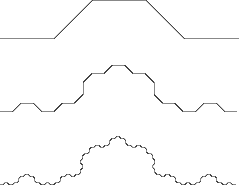
A fractal beta-skeleton with high dilation.
Beta-skeletons are graphs used, among other applications, in predicting
which pairs of cities should be connected by roads in a road network.
But if you build your road network this way, it may take you a long time
to get from point a to point b.
The isoperimetric problem for pinwheel tilings.
In these aperiodic tilings (generated by a substitution system involving
similar triangles) vertices are connected by paths almost as good
as the Euclidean straight-line distance.
Kelvin conjecture counterexample.
Evelyn Sander forwards news about the discovery by Phelan and Weaire
of a better way to partition space
into equal-volume low-surface-area cells.
Kelvin had conjectured that the truncated octahedron provided the optimal
solution, but this turned out not to be true.
See also Ruggero Gabbrielli's comparison of equal-volume partitions and
JavaView
foam models.
The Margulis Napkin Problem.
Jim Propp asked for a proof that the perimeter of a flat origami
figure must be at most that of the original starting square.
Gregory Sorkin provides a simple example showing that on the contrary,
the perimeter can be arbitrarily large.
Not. AMS
Cover, Apr. 1995. This illustration for an article on geometric
tomography depicts objects (a cuboctahedron and warped rhombic
dodecahedron) that disguise themselves as regular tetrahedra
by having the same width function or x-ray image.
A quasi-polynomial bound for the diameter of graphs of polyhedra,
G. Kalai and D. Kleitman, Bull. AMS 26 (1992). A famous open conjecture in polyhedral
combinatorics (with applications to e.g. the simplex method in linear
programming) states that any two vertices of an n-face polytope are
linked by a chain of O(n) edges. This paper gives the weaker bound
O(nlog d).
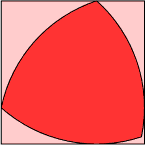
Reuleaux triangles. These curves of
constant width, formed by combining three circular arcs into an
equilateral triangle, can drill out (most of) a square hole.
Uniqueness of focal points.
A focal point (aka equichord) in a star-shaped curve is a point such that
all chords through the point have the same length.
Noam Elkies asks whether it is possible to have more than one focal point,
and Curtis McMullen discusses a generalization to non-star-shaped curves.
This problem has recently been put to rest by Marek Rychlik.
