Dilation-Free Planar Graphs

Suppose you've been hired to lay out the buildings of a college campus. College students are disrespectful of authority (at least, of campus planners) and will cut new paths through the campus lawns between any buildings not already directly connected by paths. So will the faculty. But then, wherever two paths meet, some entrepreneur is likely to place a coffee stand. This new coffee stand will attract students, who will form paths from it to all campus buildings, etc. Before long, your campus will be all covered by paths, with no lawn left. Or will it? How can you lay out your campus so that all buildings are already directly connected by paths, without forming crossroads and encouraging coffee-stand builders?

We can express this problem using the notion of dilation. The dilation of a pair of vertices in an embedded planar graph is the ratio between two kinds of distance: the length of the shortest path between them in the graph, and their geometric distance. The dilation of the graph is the maximum dilation of any two of its vertices. A graph has dilation one if and only if there is a direct path between each pair of vertices. Which graphs can have dilation one?

The pattern of solutions is common to many areas of mathematics: there are several infinite families of solutions, together with a few isolated special cases. Actually, here there is exactly one special case. First, the infinite families. Note that, if there are five or more vertices in the graph, some path must have two or more edges (there is no way to find a planar embedding of a five-vertex graph in which each vertex is connected to each other by a single edge). Let P denote the path having the most vertices; then there are four infinite families:

1. All vertices are on P:
2. One vertex is not on P:
3. Two vertices are on opposite sides of P; the path between them passes through a vertex on P: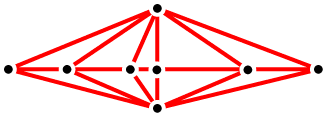
4. Two vertices are on opposite sides of the line through P; the edge between them misses P: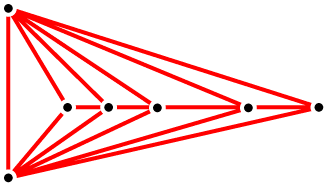

However, there is one more case: the graph can consist of a triangle nested inside another triangle, with three two-edge paths formed by two inner vertices and one outer vertex.

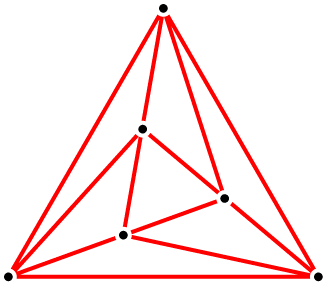
The proof that these are the only possibilities is a straightforward case analysis. If there is at most one point on either side of P, the graph is in one of the four infinite families. Otherwise, there are some two points x and y on the same side of P. If line xy passes through an endpoint of P, we can form a subset of the graph in which five points form a vee. But then, four of the points form a crossroads from which we can find a smaller vee, leading to an infinite regress. If line xy misses any vertex of P, we can form a crossroads between x, y, and two points of P, again forming a vee and an infinite regress. So, the only remaining case is that P has only three points, and that line xy passes through the middle point, forming a tee. If this is not in one of our infinite families, there must be a further point z on one side or the other of xy, and the same analysis shows that z must be one endpoint of a line through an endpoint of P and the middle point of the path containing x and y. These points together form the irregular case above, and it is not hard to see that any additional points would lead to an infinite regress.

From the Geometry Junkyard, computational and recreational geometry.
David Eppstein, Theory Group, ICS, UC Irvine.

Last update: .