It has long been known that for any two polygons of equal area (or groups of polygons adding to the same area) there is a collection of smaller polygonal pieces that can be arranged to form either of the two polygons; this partition into smaller pieces is known as a dissection. For instance, a square may be partitioned into four polygonal pieces, which can be rearranged to form an equilateral triangle of the same area. This idea was used by Hilbert to develop an axiomatic theory of plane area. Dissection has some potential application to random generation of points; it is easy to generate uniformly distributed points in a square, so by dissecting the square to another shape one can generate points in that shape. Dissection is also closely related to the Banach-Tarski paradox (which concerns itself with similar set-theoretic partitions). But problems of dissection also have more recreational aspects, concerned with minimizing the number of pieces in dissections of specific shapes.
I am interested here in a different but closely related problem: partitioning a polygon or group of polygons into a dissection such that the pieces can be rearranged to tile the plane. Each piece must be used with a density proportional to its area (otherwise one could just take a square out of the middle of one polygon and not use the other pieces). Any polygon can be dissected and rearranged to form a unit-width rectangle, so any group of polygons has a dissection tiling. Tilings have been used directly for constructing dissections (by overlaying two tilings with the same fundamental domain), but they also are useful for understanding n-to-one dissections in the limit as n grows large -- the number of pieces can be approximated by kn+O(sqrt n) where k is the average pieces/polygon in a dissection tiling. This sort of averaging allows different copies of a polygon to be cut differently; for instance we can cut two pentagons into a dissection tiling averaging 1.5 pieces/polygon whereas the best one could do with a single polygon would be 2. I depict below the best dissection tilings I know of (in terms of this average) for various regular polygons, star polygons, and groups of polygons. Since this emphasis is somewhat different from previous work on the subject, many of the dissections here are new.
Topics:
triangles --
squares --
pentagons --
hexagons --
heptagons --
octagons --
nonagons --
six-point stars --
eight-point stars --
nine-point stars --
pentagons and decagons --
pentagons and stars --
octagons and stars --
three dimensions --
bibliography.
Triangles, Squares, and Hexagons
These all tile the plane without dissection.
Pentagons
If one is given a single pentagon as input, the best one could hope to do
in a dissection tiling would be to cut it in two pieces. Many different
dissection tilings use this number of pieces. However it is possible
to achieve a better average pieces/pentagon by allowing
some pentagons to be cut differently than others:
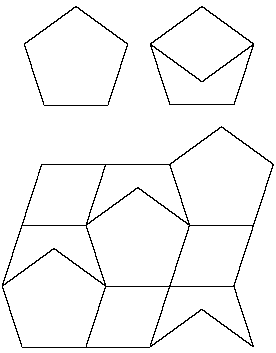
Two pentagons may be partitioned into three pieces that tile, giving an average of 1.5 pieces/polygon [original, Nov 1995].
Note that the average pieces/polygon of any pentagon dissection
tiling must be bounded away from one. To see this,
let d be the maximum density of a packing of pentagons on the plane;
then d<1. Define a piecewise constant integer function
f(x,y) by finding the piece covering (x,y) and counting
how many pieces the corresponding pentagon was cut into;
then the average pieces/polygon is just the limit of
(integral_A f(x,y) / area(A)) over larger and larger areas.
Since f(x,y) >= 1 everywhere,
and f(x,y) >= 2 on a (1-d) fraction of A,
the average pieces/polygon is at least 2-d > 1.
A similar argument applies to any input that does not itself
tile the plane.
Octagons
The octagon appears to be very stubborn.
It is easy to find a two-piece dissection
(just remove a rhomb from one corner, not shown.)
It is also possible to tile the plane with equal numbers
of undissected octagons and squares.
However I have been unable to find any
dissection tiling of multiple octagons
using fewer than two pieces/polygon.
Heptagons and Nonagons
This dissection tiling of the nonagon [original, Dec 1995], involving three different strips with straight boundaries, must be aperiodic: the strips have incommensurate periods, and one must alternate the strips in an aperiodic way to achieve the correct density of each type of piece. One can use this idea to get tilings with pieces/polygon arbitrarily close to 2.5. The same ratios are achievable by periodic tilings, by chopping the narrower strips into long pieces of commensurate lengths, and performing slide dissection on the remaining rectangular "scraps" to make them also commensurate.
One might think that an aperiodic tiling such as this one would be of no use in constructing dissections, but in fact a nine-piece dissection of the nonagon to a triangle (credited by Lindgren to Irving Freese) is related to a similar aperiodic dissection tiling in which four trapezoids are cut from the nonagon to leave an equilateral triangle. Robert Reid and Gavin Theobald further improved this dissection to eight pieces using similar methods.
The same method can also be used to find dissection
tilings of the heptagon with pieces/polygon arbitrarily close to 2
[original, Dec 1995].
Six-point Stars
There are multiple ways of partitioning a six-point star into two pieces
that tile, for instance one can simply connect two opposite reflex
vertices. However as usual the average pieces/polygon can be reduced by
dissecting several stars at once:
Three six-point stars can be dissected into five pieces
for an average of 1.666 pieces/polygon
[original, Nov 1995]. The same pieces can be arranged in other ways
(and other dissections are possible)
but this version has a pleasing amount of symmetry.
Eight-point Stars
There are two different regular eight-point stars:
8/2, in which the edges at the outer vertices point towards
vertices two points away (also formed as unions of two squares)
and 8/3, in which the edges at the outer vertices point towards
vertices three points away. More generally any star a/b
is formed with a outer corners, each connected to the next by
segments pointing in the direction of the corner b points away.
(This notation is not necessary for 5- and 6-point stars
as only one value of b is possible for them.)
This four-piece dissection tiling of the 8/2 star [original, Dec 1995] is easily generalized to tilings with average pieces/polygon arbitrarily close to 3. With a little rearrangement it can be used to find a 7-piece dissection of 8/2 to a square, different from the one by Frederickson in his book with Lindgren.
One 8/3 star can be dissected into two pieces that together tile
[credited by Grünbaum and Shephard to D. P. Chavey but not depicted there].
Nine-point Stars
One 9/3 star can be dissected into five pieces that tile
[original, Feb 1987, based on a six-piece dissection in
Grünbaum and Shephard]. Note the interesting three-way symmetry in
the tiling.
Pentagons and Decagons
Several different dissection tilings are possible for inputs
consisting of a mixture of pentagons and decagons, depending on the ratio
between the two shapes.
Four pentagons and one decagon can be dissected into six pieces for an average of 1.2 pieces/polygon [original, Nov 1995].
Fifty pentagons and eleven decagons can be dissected into seventy pieces for an average of 1.148 pieces/polygon [original, Nov 1995].
Five pentagons and one decagon can be dissected into eight pieces for an
average of 1.333 pieces/polygon [original, Nov 1995]. However
it seems likely that an even better average can be obtained by
somehow mixing the 50:11 dissection above with the 2-pentagon
dissection. This should give an average of 155/132, which is just barely
worse than 7/6, so perhaps there is a seven-piece dissection
of the same six polygons.
Pentagons and Stars
Four pentagons and one five-point star can be dissected into six pieces for an average of 1.2 pieces/polygon [original, Nov 1995]. The star can also be divided into two congruent pieces, or a pentagon can be cut and the star left intact.
Even better, ten pentagons and three stars can be dissected
into 15 pieces, for an average of 1.154 pieces/polygon [original, Dec 1995].
Octagons and Stars
There are many ways of combining octagons with 8/2 stars to form reasonably good tilings. The best one I found (in terms of the average pieces/polygon 28/23 ~ 1.2174) is formed by dissecting 17 octagons and 6 stars into 28 pieces. One of the octagons is partitioned into squares and rhombs, and the other polygons are all left intact [original, Nov 1995].
But this is not best! 14 octagons and 5 stars can be dissected into
only 23 pieces, giving a ratio of 1.2105.
[Robert Reid, July 1998].
Three Dimensional Dissection Tiling
In three dimensions, it is not true that any polyhedron has a dissection
into any other polyhedron of the same volume;
for instance the regular tetrahedron can not be dissected to
an equal-volume cube.
As a consequence, it can also not be dissected
to pieces that form a periodic tiling, because one could
then dissect a parallelohedral fundamental domain into cubes.
However it is not clear to me whether a dissection tiling
of the tetrahedron is totally ruled out by this argument, because an
aperiodic tiling (with the correct limiting density for each piece)
might still be possible.
It is known that any two zonohedra of equal volumes can be
dissected into each other. Since some zonohedra tile (e.g. the
parallelohedra and the rhombic dodecahedron), all zonohedra have
dissection tilings. However to my knowledge none have been explicitly
constructed.
Bibliography and Related Pages
David Eppstein, Inf. & Comp. Sci., UC Irvine.
Last update: