Fractals
- Allegria
fractal and mathematically inspired jewelry.
- Apollonian Gasket,
a fractal circle packing formed by packing smaller circles into each
triangular gap formed by three larger circles.
From MathWorld.
- Area of the Mandelbrot set.
One can upper bound this area by filling the area around the set by disks,
or lower bound it by counting pixels; strangely, Stan Isaacs notes,
these two methods do not seem to give the same answer.
- Balanced ternary
reptiles, Cantor's
hourglass reptile, spiral
reptile, stretchtiles,
trisection of India, the
three Bodhi problem,
and other Fractal tilings by
R. W. Gosper.
- Circle fractal
based on repeated placement of two equal tangent circles within each
circle of the figure.
One could also get something like this by inversion, starting with three
mutually tangent circles, but then the circles at each level of the
recursion wouldn't all stay the same size as each other.
- The
Curlicue Fractal, Fergus C. Murray.
- The Dynamic Systems
and Technology Project at Boston Univ. offers several Java applets
and animations of fractals and iterated function systems.
- Expansions
geometric pattern creation techniques by John S. Stokes III.
- Fractal
analysis of Jackson Pollock's abstract paintings.
- The fractal art of
Wolter Schraa. Includes some nice reptiles and sphere packings.
- Fractal bacteria.
- A fractal beta-skeleton with high dilation.
Beta-skeletons are graphs used, among other applications, in predicting
which pairs of cities should be connected by roads in a road network.
But if you build your road network this way, it may take you a long time
to get from point a to point b.
- Fractal
broccoli. Photo by alfredo matacotta.
See also this French page.
- Fractal geometry and complex bases.
Publications and software by W. Gilbert.
- Fractal instances of the traveling salesman problem, P. Moscato, Buenos Aires.
- Fractal knots, Robert Fathauer.
- Fractal patterns formed by repeated inversion of circles:
Indra's Pearls
Inversion graphics gallery, Xah Lee.
Inversive circles, W. Gilbert, Waterloo.
- Fractal patterns
in the real world, Ian Stewart.
- Fractal
planet and fractal
landscapes. Felix Golubov makes random triangulated polyhedra in Java
by perturbing the vertices of a recursive subdivision.
- Fractal
reptiles and other
tilings by IFS
attractors, Stewart Hinsley.
- Fractal
resources. A collection of web links by John Mathews.
- Fractal tilings.
- Fractals.
The spanky fractal database at Canada's national meson research facility.
- Generating
Fractals from Voronoi Diagrams, Ken Shirriff, Berkeley and Sun.
- Geometric
Arts. Knots, fractals, tesselations, and op art.
Formerly Quincy
Kim's World of Geometry.
- IFS and L-systems.
Vittoria Rezzonico grows fractal broccoli and Sierpinski pyramids.
- Sándor Kabai's
mathematical graphics, primarily polyhedra and 3d fractals.
- Robert
F. Kauffman's fractal and Escherian art, with
Escher-like animated animal-form tilings.
- Labyrinth tiling.
This aperiodic substitution tiling by equilateral and isosceles triangles
forms fractal space-filling labyrinths.
- Mathematical imagery by Jos Leys.
Knots, Escher tilings, spirals, fractals, circle inversions, hyperbolic
tilings, Penrose tilings, and more.
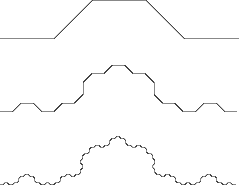
- Line fractal.
Java animation allows user control of a fractal formed by repeated
replacement of line segments by similar polygonal chains.
- Number patterns,
curves, and topology, J. Britton.
Includes sections on the golden ratio, conics, Moiré patterns,
Reuleaux triangles, spirograph curves, fractals, and flexagons.
- Paperfolding
and the dragon curve. David Wright discusses the connections
between
the dragon fractal,
symbolic dynamics, folded pieces of paper, and
trigonometric sums.
- Pi and the Mandelbrot set.
- Pleats, twists, and
sliceforms. Some links to Richard Sweeney's fractal paperfolding
art, via dataisnature.
- Programming for 3d
modeling, T. Longtin. Tensegrity structures, twisted torus space frames,
Moebius band gear assemblies, jigsaw puzzle polyhedra, Hilbert fractal helices,
herds of turtles, and more.
- Rational
maps with symmetries.
Buff and Henriksen investigate rational functions invariant under
certain families of Möbius transformations, and use them to
generate symmetric Julia sets.
- Reproduction of
sexehexes. Livio Zucca finds an interesting fractal polyhex based on
a simple matching rule.
- Vittoria Rezzonico's
Java applets. Hypercube and polyhedron visualization, and circle
inversion patterns. Requires both Java and JavaScript.
- Sierpinski carpet on the sphere.
From Curtis McMullen's
math gallery.
- The Sierpinski Tetrahedron, everyone's
favorite three dimensional fractal.
Or is it a fractal?
- sneJ made a
Mandelbrot set with sheet plastic and a laser cutter.
-
Spherical
Julia set with dodecahedral symmetry
discovered by McMullen and Doyle in their work on
quintic equations and rendered by
Don Mitchell.
Update 12/14/00: I've lost the big version of this image and can't find
DonM anywhere on the net -- can anyone help?
In the meantime, here's a link to
McMullen's
rendering.
- 3D strange attractors and similar objects, Tim Stilson, Stanford.
- What happens when you
connect uniformly spaced but not dyadic rational points along the Peano
spacefilling curve? R. W. Gosper illustrates the results.
- Yantram sacred art toolbox.
Software for creating various kinds of symmetric fractal mandala.
From the Geometry Junkyard,
computational
and recreational geometry pointers.
Send email if you
know of an appropriate page not listed here.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Semi-automatically
filtered
from a common source file.