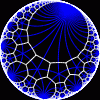
Tilings of Hyperbolic Spaces

• Dehn invariants of hyperbolic tiles. The Dehn invariant is one way of testing whether a Euclidean polyhedron can be used to tile space. But as Doug Zare describes, there are hyperbolic tiles with nonzero Dehn invariant.

• Do buckyballs fill hyperbolic space?

• Gallery of interactive on-line geometry. The Geometry Center's collection includes programs for generating Penrose tilings, making periodic drawings a la Escher in the Euclidean and hyperbolic planes, playing pinball in negatively curved spaces, viewing 3d objects, exploring the space of angle geometries, and visualizing Riemann surfaces.

• Gaussian continued fractions. Stephen Fortescue discusses some connections between basic number-theoretic algorithms and the geometry of tilings of 2d and 3d hyperbolic spaces.

• D. Huson's favorite hyperbolic tiling.

• Hyperbolic geometry. Visualizations and animations including several pictures of hyperbolic tessellations.

• Hyperbolic shortbread. The Davis math department eats a Poincaré model of a tiling of the hyperbolic plane by 0-60-90 triangles.

• The hyperbolic surface activity page. Tom Holroyd describes hyperbolic surfaces occurring in nature, and explains how to make a paper model of a hyperbolic surface based on a tiling by heptagons.

• Hyperbolic Tessellations, David Joyce, Clark U.

• Hyperbolic tiles. John Conway answers a question of Doug Zare on the polyhedra that can form periodic tilings of 3-dimensional hyperbolic space.

• Hyperbolic and spherical tiling gallery, Bernie Freidin.

• Hyperbolic planar tessellations, image gallery of many regular and semiregular tilings by Don Hatch.
  

• Mathematical imagery by Jos Leys. Knots, Escher tilings, spirals, fractals, circle inversions, hyperbolic tilings, Penrose tilings, and more.

• More hyperbolic tilings and software for creating them, J. Mount.

• Pavages hyperboliques dans le modèle de Poincaré. Animated with CabriJava. Includes separate pages on hyperbolic tilings with regular polygons including squares, pentagons, and hexagons.

• Penguins on the hyperbolic plane, Misha Kapovich. See also his Escher-like Crocodiles on the Euclidean plane.

• Two-three-seven tiling of the hyperbolic plane with lines that connect to give a fiery appearance. From the Geometry Center archives.

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein, Theory Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file.