Pentagonal Geometry and the Golden Ratio
This page includes geometric problems defined on regular pentagons, involving pentagonal angles, or based on the golden ratio (the ratio of diagonal to side length in a regular pentagon).
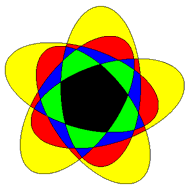
A Brunnian link. Cutting any one of five links allows the remaining four to be disconnected from each other, so this is in some sense a generalization of the Borromean rings. However since each pair of links crosses four times, it can't be drawn with circles.
Constructing a regular pentagon inscribed in a circle, by straightedge and compass. Scott Brodie.
Cut-the-knot logo. With a proof of the origami-folklore that this folded-flat overhand knot forms a regular pentagon.
The downstairs half bath. Bob Jenkins decorated his bathroom with ceramic and painted pentagonal tiles.
Equilateral pentagons. Jorge Luis Mireles Jasso investigates these polygons and dissects various polyominos into them.
Equilateral pentagons that tile the plane, Livio Zucca.
The golden ratio in an equilateral triangle. If one inscribes a circle in an ideal hyperbolic triangle, its points of tangency form an equilateral triangle with side length 4 ln phi! One can then place horocycles centered on the ideal triangle's vertices and tangent to each side of the inner equilateral triangle. From the Cabri geometry site. (In French.)
The golden section and geometry. Somehow leading to questions like how many stars there are on the US flag.
Golden rectangles, Curtis McMullen.
A golden sales pitch. Julie Rehmeyer dissects the myth of the golden ratio in classical art and describes some new uses for it in commerce.
The golden section and Euclid's construction of the dodecahedron, and more on the dodecahedron and icosahedron, H. Serras, Ghent.
Golden spiral flash animation, Christian Stadler.
How many points can one find in three-dimensional space so that all triangles are equilateral or isosceles? One eight-point solution is formed by placing three points on the axis of a regular pentagon. This problem seems related to the fact that any planar point set forms O(n7/3) isosceles triangles; in three dimensions, Theta(n3) are possible (by generalizing the pentagon solution above). From Stan Wagon's PotW archive.
How to construct a golden rectangle, K. Wiedman.
Isotiles, workbook on the shapes that can be formed by combining isosceles triangles with side lengths in the golden ratio.
Jiang Zhe-Ming's geometry challenge. A pretty problem involving cocircularity of five points defined by circles around a pentagram.
Largest 5-gon in a square, or more interestingly smallest equilateral pentagon inscribed in a square. Posting to sci.math by Rainer Rosenthal.
Lattice pentagons. The vertices of a regular pentagon are not the subset of any lattice.
Miquel's pentagram theorem on circles associated with a pentagon. With annoying music.
Number patterns, curves, and topology, J. Britton. Includes sections on the golden ratio, conics, Moiré patterns, Reuleaux triangles, spirograph curves, fractals, and flexagons.
Parallel pentagons. Thomas Feng defines these as pentagons in which each diagonal is parallel to its opposite side, and asks for a clean construction of a parallel pentagon through three given points. (He is aware of the obvious reduction via affine transformation to the construction of regular pentagons, but finds that non-elegant.)
Penrose mandala and five-way Borromean rings.
Penrose tilings. This five-fold-symmetric tiling by rhombs or kites and darts is probably the most well known aperiodic tiling.
Perplexing pentagons, Doris Schattschneider, from the Discovering Geometry Newsletter. A brief introduction to the problem of tiling the plane by pentagons.
Pentagon packing on a circle and on a sphere, T. Tamai.
Pentagonal Tessellations. John Savard experiments with substitution systems to produce tilings resembling Kepler's.
Pentagons that tile the plane, Bob Jenkins. See also Ed Pegg's page on pentagon tiles.
The pentagram and the golden ratio. Thomas Green, Contra Costa College.
Russian math olympiad problem on lattice points. Proof that, for any five lattice points in convex position, another lattice point is on or inside the inner pentagon of the five-point star they form.
A Venn diagram made from five congruent ellipses. From F. Ruskey's Combinatorial Object Server.
Wonders of Ancient Greek Mathematics, T. Reluga. This term paper for a course on Greek science includes sections on the three classical problems, the Pythagorean theorem, the golden ratio, and the Archimedean spiral.
