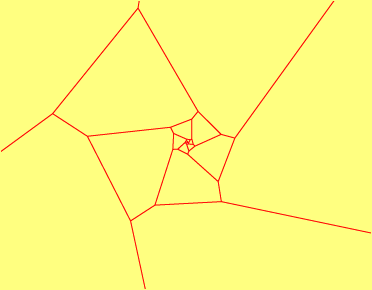
A well-known example of such a spiral tiling is formed by squares, with adjacent squares in the spiral having sizes in the golden ratio to each other.
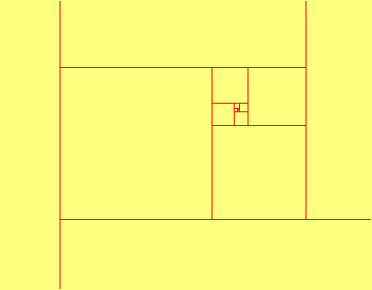
A related tiling using a 1 by sqrt(2) rectangle is the basis for European paper size standards, and K. S. Brown's page on "the golden triangle" hints at the existence of another tiling with equilateral triangles the size ratio of which is a root of the polynomial x3-x-1. Brown's web site also includes a description of another spiral tiling by 30-60-90 right triangles.
What is a good definition of a spiral tiling? What shapes can be used as the tiles in spiral tilings? How many neighbors can each tile have? What are the symmetries of these tilings?
The same combination of motions arises in multiplying complex numbers a+bi. If we think of these numbers as forming a plane, then multiplying all the points of any configuration in that plane by a+bi can be carried out geometrically, by expanding the configuration away from the origin by a factor of sqrt(a2+b2), and simultanously twisting the configuration around the origin by an angle of tan-1(a/b).
For this reason it makes sense to use complex number multiplication to represent the symmetries of a spiral tiling.
We define a tile to be an open connected subset of the complex number plane.
We define a tiling to be a set of disjoint tiles, the closure of which covers the entire complex number plane.
We define a complex symmetry of a tiling to be a complex number such that multiplying each tile by that number produces another tile of the same tiling.
We define a spiral tiling to be a tiling in which for any two tiles s and t, some complex symmetry of the tiling maps s to t.
The last definition can be rephrased as saying that the symmetries act transitively on the tiles. Note that these definitions are different from the notion of a spiral tiling used by Grünbaum and Shephard [Tilings and Patterns, W.H. Freeman 1987, pp. 512-516], which does not involve similarity and is generally rather less well-defined than the above (the "I know it when I see it" test applies). Some material closer to what we have here can be found in the same book [pp. 520-522].
Consider the distances d(s) and d(t) of each from the origin. Since complex multiplication acts on these distances, the magnitude of z must be d(t)/d(s). What about its orientation?
Suppose s*y=s*z=t. Then s*(z/y)=s, so s is invariant by some rotation about the origin. The only such tiles can be annuli in which the two boundary components are similarly invariant and similar to each other.

We treat this case as degenerate; from now on we assume that it does not occur in our tilings. So in a non-degenerate spiral tiling, the symmetry z mapping s to t is uniquely defined. We denote this symmetry by t/s.
If we choose a reference point 1 in some tile containing that point, the images of that point 1*G=G give one reference point in each tile, so the members of G are in one-to-one correspondence with the tiles of the spiral tiling. We can think of each tile as forming a canonical neighborhood or fundamental domain around each symmetry z.
There is a slight complication: exp(z) is not one-to-one, since exp(z)=exp(z+2pi). Therefore a more-or-less arbitrary choice has to be made about which value to use as the inverse. In our case, we are interested in set-theoretic inverses, so we use the notation log(G) to denote the set { z : exp(z) in G }.
Then if G is a multiplicative subgroup of the complex numbers, log(G) is an additive subgroup. And if G is a discrete set, log(G) is also discrete. So if G is the set of symmetries of a spiral tiling, log(G) is a discrete subgroup of the additive complex numbers. There are only two possibilities for what such a subgroup can look like: either it is a lattice, or it is the set of integer multiples Kz of a single generator z.
Note finally that 2 pi i is a member of log(G), since it is in log(1). So if log(G) is a lattice, it is a lattice containing the vector 2 pi i. And if log(G) is of the form Kz, then z must be purely imaginary, so G (which consists of the powers of exp(z)) must consist purely of rotations. If so, we have another degenerate case in which some finite number of infinite wedges tile the plane by fitting together at the origin.
Therefore from now on, we can assume that any non-degenerate spiral tiling is of the form exp(T) where T is a periodic (congruence) tiling having a translation by 2 pi i among its lattice of translational symmetries.
In more detail, if one glues the edges of the tile together in a pattern formed by how it connects to its neighbors, one gets a manifold, a space which near each point "looks like" the plane. The analysis above, showing that the tiling comes from applying the exponential map to a periodic tiling, shows that this manifold must be topologically equivalent to a torus, so Euler's formula tells us that V-E+F=0, where F is the number of faces in the manifold (just one), E is the number of edges, and V is the number of vertices. Now if the tile has k neighbors, it contributes k sides of edges to E, but each edge has two sides so E=k/2 and k must be even. Further, each vertex has at least three ends of edges, and each edge has two ends, so 2E<=3V, which combined with Euler's formula E=V+1 implies that E<=3.
The case that k=2 gives us our third type of degenerate tiling. This case occurs when the lattice log(G) is generated by the two values pi i and x for some real x, so the only symmetries of the tiling are expansions (without rotation) and reflection through the origin. The tiles in this degenerate case must be infinite strips, the two boundaries of which are similar to each other.

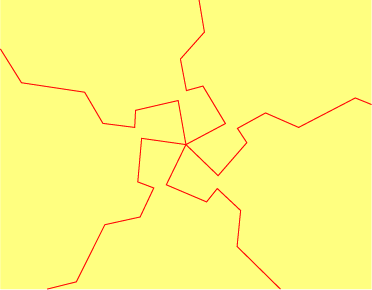
In the remaining cases, the tiles are combinatorially equivalent to quadrilaterals or hexagons (they may take other shapes, including triangles and pentagons, but they have either four or six neighbors, and are adjacent to four or six vertices where more than two tiles meet). This is a key difference from periodic tilings, which also allow tiles with three neighbors.
As described by Thurston [Three-Dimensional Geometry and Topology, unpublished manuscript, 1990, p. 137] any quadrilateral can be fitted into similar copies of itself in a way that locally looks like part of a spiral tiling. This construction is known as the "developing map" and is a special case of a construction that works for arbitrary manifolds. However, there are some nonlocal requirements on the shape of quadrilaterals that form spiral tilings. If one applies the developing map construction to an arbitrary quadrilateral, the result usually overlaps itself or has cracks that can not be filled.
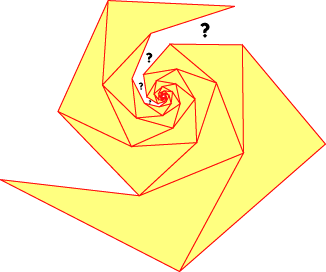
The space of all quadrilateral shapes can be specified by four parameters (e.g. two angles and two edge lengths). It seems that the requirement that the developing map meets up with itself corresponds to a restriction to a two-dimensional subspace of the quadrilateral shapes. Is there a reasonable way to describe that subspace?
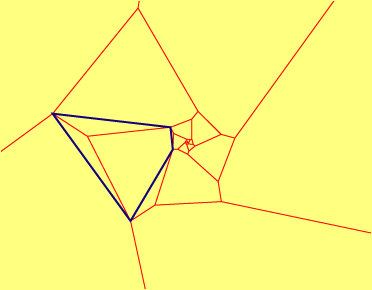
So it must be possible to dissect the hexagon into pieces that can be reassembled (allowing similarity) into a quadrilateral that forms a spiral tiling. One simple necessary condition for the tiling to exist is that one must be able to group the hexagon vertices into two triples, each triple adding to 2 pi. Do these two triples have to alternate around the hexagon, as they do in the tiling above? What other conditions are necessary?
From the Geometry Junkyard,
computational and recreational geometry.
David Eppstein, Theory Group, ICS, UC
Irvine.
Last update: .