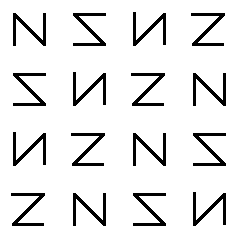
Symmetry and Group Theory

• The Aesthetics of Symmetry, essay and design tips by Jeff Chapman.

• Antipodes. Jim Propp asks whether the two farthest apart points, as measured by surface distance, on a symmetric convex body must be opposite each other on the body. Apparently this is open even for rectangular boxes.

• Associating the symmetry of the Platonic solids with polymorf manipulatives.

• Border pattern gallery. Oklahoma State U. class project displaying examples of the seven types of symmetry (frieze groups) possible for linear patterns in the plane.

• Cognitive Engineering Lab, Java applets for exploring tilings, symmetry, polyhedra, and four-dimensional polytopes.

• Conceptual proof that inversion sends circles to circles, G. Kuperberg.

• Convex Archimedean polychoremata, 4-dimensional analogues of the semiregular solids, described by Coxeter-Dynkin diagrams representing their symmetry groups.

• Crystallographic topology. C. Johnson and M. Burnett of Oak Ridge National Lab use topological methods to understand and classify the symmetries of the lattice structures formed by crystals. (Somewhat technical.)

• Crystallography now, tutorial on the seventeen plane symmetry groups by George Baloglou.

• Diamond theory. Steven Cullinane studies the symmetries of the shapes formed by splitting each square of a grid into dark and light triangles.

• Dreamscope screen-saver module makes patterns with various Kaleidoscopic symmetries.

• Escher's combinatorial patterns, D. Schattschneider, Elect. J. Combinatorics.

• Michael Field's gallery of symmetric chaos images. See his home page for more links to pages on dynamics, symmetry, and chaos.

• Figure eight knot / horoball diagram. Research of A. Edmonds into the symmetries of knots, relating them to something that looks like a packing of spheres. The MSRI Computing Group uses another horoball diagram as their logo.

• Fractal patterns formed by repeated inversion of circles: Indra's Pearls Inversion graphics gallery, Xah Lee. Inversive circles, W. Gilbert, Waterloo.
  

• Gavrog, a Java package for visualizing 2d and 3d ornamental patterns with high degrees of symmetry.

• Geometry and the Imagination in Minneapolis. Notes from a workshop led by Conway, Doyle, Gilman, and Thurston. Includes several sections on polyhedra, knots, and symmetry groups.

• The Graph of the Truncated Icosahedron and the Last Letter of Galois, B. Kostant, Not. AMS, Sep. 1995. Group theoretic mathematics of buckyballs. See also J. Baez's review of Kostant's paper.

• Hecatohedra. John Conway discusses the possible symmetry groups of hundred-sided polyhedra.
  

• The icosahedron, the great icosahedron, graph designs, and Hadamard matrices. Notes by M. Brundage from a talk by M. Rosenfeld.

• Investigating Patterns: Symmetry and Tessellations. Companion site to a middle school text by Jill Britton, with links to many other web sites involving symmetry or tiling.

• Jenn open-source software for visualizing Cayley graphs of Coxeter groups as symmetric 4-dimensional polytopes.

• Joe's Cafe. Java applets for creating images of iteration systems a la Field and Golubitsky's "Symmetry in Chaos".

• K12 on G6. Carlo Séquin investigates how to draw a 12-vertex complete graph as symmetrically as possible on a six-handle surface (the minimum genus surface on which it can be drawn without crossings).

• Kaleidoscope geometry, Ephraim Fithian.

• Kali, software for making symmetrical drawings based on any of the 17 plane tiling groups.

• Kummer's surface. Nice ray-traced pictures of a quartic surface with lots of symmetries.

• MagicTile. Klein's quartic meets the Rubik's cube, by Roice Nelson.

• Mirror Curves. Slavik Jablan investigates patterns formed by crisscrossing a curve around points in a regular grid, and finds examples of these patterns in art from various cultures.

• Models of Platonic solids and related symmetric polyhedra.

• Moebius transformations revealed. Video by Douglas N. Arnold and Jonathan Rogness explaining 2d Moebius transformations in terms of the motions of a 3d sphere. See also MathTrek.

• Origami: a study in symmetry. M. Johnson and B. Beug, Capital H.S.

• Parabolic isometry of an ideal hyperbolic triangulation. Animation by John Griffin.

• Platonic solids and quaternion groups, J. Baez.

• Platonic spheres. Java animation, with a discussion of platonic solid classification, Euler's formula, and sphere symmetries.

• Platonic tesselations of Riemann surfaces, Gerard Westendorp.

• ProtoZone interactive shockwave museum exhibits for exploring geometric concepts such as symmetry, tiling, and wallpaper groups.

• Puzzles with polyhedra and numbers, J. Rezende. Some questions about labeling edges of platonic solids with numbers, and their connections with group theory.

• Rational maps with symmetries. Buff and Henriksen investigate rational functions invariant under certain families of Möbius transformations, and use them to generate symmetric Julia sets.

• Rhombic tilings. Abstract of Serge Elnitsky's thesis, "Rhombic tilings of polygons and classes of reduced words in Coxeter groups". He also supplied the picture below of a rhombically tiled 48-gon, available with better color resolution from his website.
  

• Sighting point. John McKay asks, given a set of co-planar points, how to find a point to view them all from in a way that maximizes the minimum viewing angle between any two points. Somehow this is related to monodromy groups. I don't know whether he ever got a useful response.

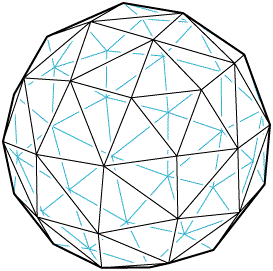
• Soccer ball pictures, spherical patterns generated by reflections that form rational angles to each other.

• Spherical Julia set with dodecahedral symmetry discovered by McMullen and Doyle in their work on quintic equations and rendered by Don Mitchell. Update 12/14/00: I've lost the big version of this image and can't find DonM anywhere on the net -- can anyone help? In the meantime, here's a link to McMullen's rendering.
  

• Steve's sprinklers. An interesting 3d polygon made of copper pipe forms various symmetric 2d shapes when viewed from different directions.

• Wilson Stothers' Cabri pages. Geometric animations teaching projective conics, hyperbolic geometry, and the Klein view of geometry as symmetry.

• SymmeToy, windows shareware for creating paint patterns, symmetry roses, tessellated art and symmetrically decorated 3D polyhedron models.

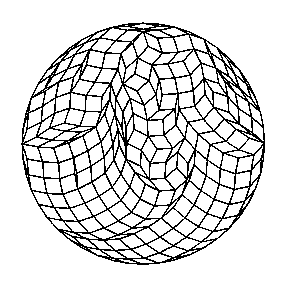
• Symmetries of torus-shaped polyhedra

• Symmetry, tilings, and polyhedra, S. Dutch.

• Symmetry and Tilings. Charles Radin, Not. AMS, Jan. 1995. See also his Symmetry of Tilings of the Plane, Bull. AMS 29 (1993), which proves that the pinwheel tiling is ergodic and can be generated by matching rules.

• Symmetry in Threshold Design in South India.

• Symmetry web, an exploration of the symmetries of geometric figures.

• Tales of the dodecahedron, from Pythagoras to Plato to Poincaré. John Baez, Reese Prosser Memorial Lecture, Dartmouth, 2006.

• Taprats Java software for generating symmetric Islamic-style star patterns.

• Temari dodecahedrally decorated Japanese thread ball. See also Summer's temari gallery for many more.

• Morwen Thistlethwait, sphere packing, computational topology, symmetric knots, and giant ray-traced floating letters.

• Thoughts on the number six. John Baez contemplates the symmetries of the icosahedron.

• TileDreams Windows software for creating symmetric patterns with rhombi.

• Tiling the integers with one prototile. Talk abstract by Ethan Coven on a one-dimensional tiling problem on the boundary between geometry and number theory, with connections to factorization of finite cyclic groups. See also Coven's paper with Aaron Meyerowitz, Tiling the integers with translates of one finite set.

• Tilings. Lecture notes from the Clay Math Institute, by Richard Stanley and Federico Ardila, discussing polyomino tilings, coloring arguments for proving the nonexistence of tilings, counting how many tilings a region has, the arctic circle theorem for domino tilings of diamonds, tiling the unit square with unit-fraction rectangles, symmetry groups, penrose tilings, and more. In only 21 pages, including the annotated bibliography. A nice but necessarily concise introduction to the subject. (Via Andrei Lopatenko.)

• Tilings and visual symmetry, Xah Lee.

• Transformational geometry. Leslie Howe illustrates various plane symmetry types with Cabri animations.

• The uniform net (10,3)-a. An interesting crystal structure formed by packing square and octagonal helices.

• Vision test. Can you spot the hidden glide reflection symmetry lurking in (the infinite continuation of) this pattern?
  

• Wallpaper groups. An illustrated guide to the 17 planar symmetry patterns. See also Xah Lee's wallpaper group page.

• Wallpaper patterns, R. Morris. Kaleidoscope-like Java applet for making and transforming symmetric tilings out of uploaded photos.

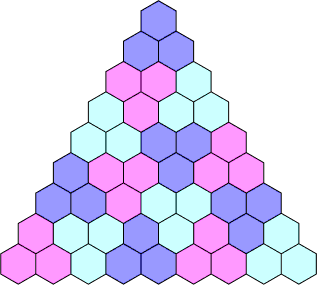
• A word problem. Group theoretic mathematics for determining whether a polygon formed out of hexagons can be dissected into three-hexagon triangles, or whether a polygon formed out of squares can be dissected into restricted-orientation triominoes.
  

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein, Theory Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file.