
ICS 180, Winter 1999:
Strategy and board game programming
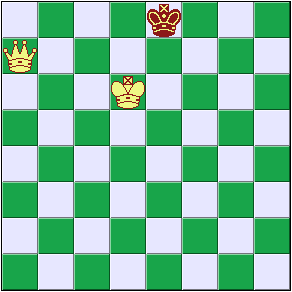
For example, consider the following chess position:

White to move can win immediately by moving the queen to square e7, checkmating the black queen. But white also has other moves that win more slowly; in fact there is only one move white can make that does not win. For instance, suppose white moves his king to e6; black's only moves are d8 and f8, after either of which white still has a checkmate possible. If black moves to d8, white can still win by moving back to d6. But after the sequence of moves 1. Ke6 Kd8 2. Kd6 Ke8 we are back where we started! White is making winning moves, but he isn't making progress to a win.
If an alpha-beta search gives the same evaluation to any winning position, it can easily fall into this trap. To prevent this, we need to change the evaluation of winning positions, so that a win in fewer moves is counted slightly better than a delayed win. The code is straightforward: if we keep a variable "ply" denoting how far the current position is from the root of the search, we can adjust the score for a winning position by subtracting the ply. The following pseudocode assumes that we have defined a constant "WIN" which refers to the maximum score possible in a game (in chess, a typical value for WIN would be 100 or 1000 times the value of a pawn).
// Alpha-beta search with WIN scores adjusted for ply
int ply; // global variable initialized to zero at start of search
int alphabeta(int depth, int alpha, int beta)
{
if (game over and current player has won) return WIN - ply;
else if (game over and current player has lost) return -WIN + ply;
else if (depth <= 0) return eval();
ply++;
for (each possible move m) {
make move m;
alpha = max(alpha, -alphabeta(depth - 1, -beta, -alpha);
unmake move m;
if (alpha >= beta) break;
}
ply--;
return alpha;
}
Now in the example above, the immediate checkmate is seen at ply=1,
and gets a score of 999 (WIN-1), while moving the king to e8 forces a win
at ply=3, with a score of 997. The program will move to the position
maximizing its score, and take the immediate checkmate.
For some games, such as Othello, there is a natural limit to the length of the game: each move adds a piece to the board, so there can be at most 64 moves before the game finishes. For those games, there is no way to get into the same sort of infinite loop, and we can just use a score of WIN or -WIN without worrying about the ply adjustment.
There is one further complication with this ply adjustment trick: how does it interact with the hash table? The problem is that the ply may differ between the time we store a move in the hash table, and the time we retrieve it. In order to make the retrieved score's ply adjustment correct, we should store scores in the hash table adjusted relative to the current position, rather than the position at the root of the search.
That is, when storing a position in the hash table, use something like the following pseudocode, where MAX_PLY is a constant defined to be greater than the maximum depth possible in a search (WIN=1000 and MAX_PLY=100 might be reasonable). The variable x is just the index of the current position in the hash table.
if (score > WIN - MAX_PLY) hash[x].score = score + ply;
else if (score < -WIN + MAX_PLY) hash[x].score = score - ply;
else hash[x].score = score;
When retrieving a position from the hash table, the opposite adjustment needs to be made:
if (hash[x].score > WIN - MAX_PLY) score = hash[x].score - ply;
else if (hash[x].score < -WIN + MAX_PLY) score = hash[x].score + ply;
else score = hash[x].score;