Coloring Line Arrangements

If one places an arrangement of lines in the plane, it forms a graph in which the vertices correspond to places where two or more lines cross and the edges correspond to the line segments connecting the vertices. How many colors do we need to color such a graph?

As it turns out, there are several different versions of the problem, depending on our assumptions. Is the arrangement simple (containing no three lines that meet at a single point)? Do we count as edges the connections that wrap around "through infinity" connecting the first and last crossings on each line? We might also ask whether we allow parallel lines or not, but unlike the previous two questions this does not seem to be important in determining the chromatic number of line arrangements.

Simple arrangements without wraparound

We first consider the graphs arising from simple arrangements, in which we do not allow wraparound edges. In this case a simple greedy algorithm shows that the chromatic number is at most three. We can assume (by rotating the arrangement if necessary) that no line is vertical. Then simply color the vertices from left to right. Each vertex has at most two neighbors already colored, so one of three colors is always available. It is also easy to construct arrangements requiring three colors.

Non-simple arrangements without wraparound

Without wraparound, a planar line arrangement forms a planar graph, so the four-color theorem tells us its chromatic number is at most four. The following example shows that four colors are sometimes needed (the arrangement contains other intersections outside the ones shown, that are not necessary to determine the chromatic number):

Simple arrangements with wraparound

Wrapping edges "through infinity" to connect the first and last vertices on each line causes some complications in coloring the arrangement. The resulting graph is no longer planar: if we tried to draw the wrapped around connections we would find that they cross each other. Instead the arrangement lives on a surface other than the usual Euclidean plane, known as the "projective plane", which differs somewhat in its properties. For instance the four-color theorem does not apply to projective-planar graphs; instead they may require up to five colors. However only four colors are needed for simple arrangements with wraparound.

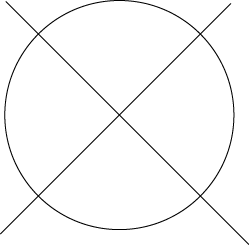
To see this, note that any simple arrangement forms a graph in which each vertex has exactly four neighbors. A well-known result in graph theory (Brooks' theorem) states that if the vertices in a graph have at most k neighbors, and the graph is neither complete nor an odd cycle, then the graph is k-colorable. In our case, an odd cycle clearly has fewer than four neighbors per vertex, so the only other problem case would be the complete graph K₅. And although K₅ can be embedded on the projective plane (one embedding is shown below) it can not come from a line arrangement, since its does not have a triangular number of vertices. (A simple n-line arrangement has exactly n(n-1)/2 vertices.)

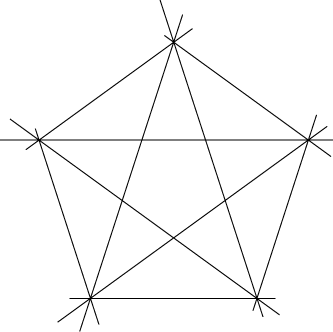
So Brooks' theorem tells us that four colors suffice to color simple arrangements with wraparound. The following example shows a matching lower bound: at least four colors may be required.

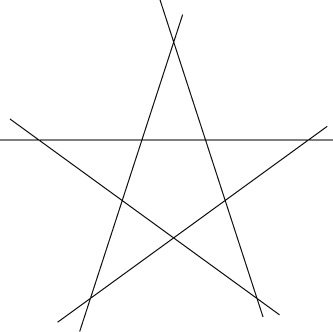
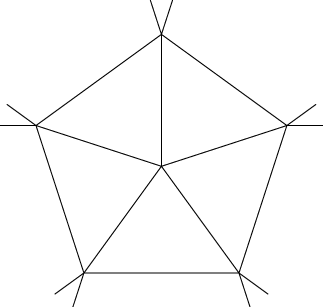
Non-simple arrangements with wraparound

Any graph in the projective plane can be colored with at most six colors. (One relatively easy way to see this is to use Euler's formula to show that there exists a vertex of degree at most five; therefore one can remove that vertex, color the remaining graph recursively, and then add the vertex back with at least one color available to color it.) And some projective-planar graphs, for instance, the following complete graph on six vertices, require six colors.

This graph's vertices have odd numbers of neighbors so it does not come from a line arrangement. The following example (known in projective geometry as the "complete quadrangle") shows that five colors may sometimes be needed for the graphs coming fromline arrangements. The three outer vertices and the center one are all connected to each other, and so require four different colors. The remaining three vertices are each connected to these four and require a fifth color.

We now sketch a proof that five colors are always sufficient. A line arrangement always has a degree-four vertex (Sylvester's theorem); this can be seen by applying Euler's formula to show that there exists a vertex of degree at most five, but then observing that all vertex degrees are even. So, let v be such a vertex, contained on line L.

Form a graph G by collapsing all vertices on line L into a single point; then G is a planar graph. More technically, L can be assumed to be the "line at infinity" of the projective plane, and the collapse of L produces the "one-point completion" of the Euclidean plane, which is just a sphere, and graphs embedded on the sphere are always planar. So by the four-color theorem G can be colored with at most four colors.

If we undo the collapse, to get back to the line arrangement we're interested in coloring, then everything on L will be colored the same color, say red, L will have no red neighbors, and the rest of the arrangement will be colored ok. We now recolor the vertices on L to make a five-coloring of the whole arrangement. Because we've only used four colors so far, one color, say blue, is still unused. The vertices on L form a cycle, which can be thought of as a path connected at its endpoints by the special vertex v. We simply change the color of every other vertex on that path from red to blue. Finally, we need to choose a color for v. If L has an odd number of vertices, one neighbor of v on L might be red and one might be blue. But only two of the three remaining colors can be used by the other two neighbors of v, so there is always some color available to color v and complete the five-coloring of the arrangement.

Summary

We have described coloring problems for simple and non-simple line arrangements, with and without edges that wrap around through infinity. Simple arrangements without wraparound have chromatic number three. Non-simple arrangements without wraparound have chromatic number four. Simple arrangements with wraparound have chromatic number four. And non-simple arrangements with wraparound have chromatic number five.

From the Geometry Junkyard, computational and recreational geometry.
David Eppstein, Theory Group, ICS, UC Irvine.

Last update: .