The three most common methods for interactive display of three dimensional objects on the web seem to be the Virtual Reality Modeling Language (VRML), Apple's Quicktime VR (QTVR), and Java. All can be used with Netscape or other browsers on both Windows and Mac platforms; Java also works on Unix machines but the other two apparently do not. VRML represents three-dimensional objects directly, with an interface allowing the objects and point of view to both move, but is limited to displaying only three dimensional Euclidean space and (because it must be rendered in realtime) can only do certain primitive types of rendering. Since Java is a programming language, it can (theoretical) display anything, and its user interface controls need not correspond directly to camera motion; its limits are set by programmer competence and the same realtime rendering problem that besets VRML. QTVR objects are formed simply from a set of precomputed image frames, so it is as unlimited as Java in the types of object it can display, it doesn't require as much programming effort, and it also avoids the realtime rendering bottleneck of the other two methods. QTVR's user interface only provides for two degrees of freedom but those degrees of freedom can like Java be used to control any parameter, not just camera motion. Therefore QTVR seems the most flexible option for mathematical visualizations requiring only limited user interaction. (QTVR also excels in viewing photographic or photographic-quality images such as fashion modeling, landscapes, and architectural walkthroughs.) However, QTVR's bandwidth requirements are typically much higher than the other methods.
Herewith my efforts in the use of QTVR for mathematical visualization.
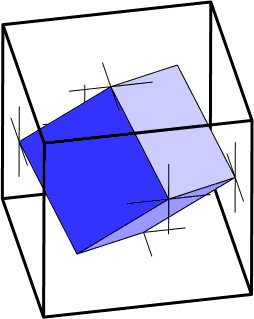
Later, I redid this drawing as a raytraced rendering. Some of the complications here included making the outer box look transparent, but not distorting the inner box's shape, and still making it possible to visualize the outer shape. I used POV-Ray's glass texture, modified to turn off refraction, increase surface roughness, and decrease the amount of specular reflection. The image size is about 2/3 that of the original line art, and to the eye looks even smaller (more like 1/2 the size); the more realistic rendering helps make up for the loss in size, but the animated GIF's constant motion is distracting. The QTVR version has better color resolution than the GIF, allows for a greater variety of viewpoints, and allows the user to understand the shape better by controlling the direction from which it is viewed.

Technical details: Rendered by POV-Ray, converted to animated GIF and QTVR by GIFbuilder 0.5, ConvertToMovie 1.6, Make QTVR Object 1.0b4, and a simple AppleScript program for renaming POV-Ray output files to the names expected by ConvertToMovie. Views were chosen with 6 degrees of separation, decreased from QTVR's recommendation of 10 for greater smoothness of rotation. Vertical camera angle ranges from 0 to 66 degrees (20 degrees for the GIF). Because of the symmetry of the configuration, rendering only needed to be done through a 120 degree horizontal rotation, saving a factor of 3 in file size and rendering time. Even so, the 240 frames in the full QTVR object use 4MB of storage and took 6 1/2 hours to render on a 200MHz PowerPC 603. This was my first QTVR project, and my first animated GIF, so I spent a lot of time trying different image compression options, color maps, and so on, finally settling on dithering for the GIF and JPEG compression (100% quality) for the QTVR frames. Lower quality JPEGs were smaller but made the inner cube's edges blurry; ConvertToMovie's "Graphics" option was my second choice for QTVR image format.
I made these as demos for a graduate seminar on mesh generation, to be viewed in class on my laptop computer, so the movies are large (both in pixels, 400x400, and in bytes, 6M to 9M). Due to time and space limitations I only rendered one degree of freedom.
 Schönhardt polyhedron:
Schönhardt polyhedron:QTVR (6M); POV-Ray source (2k) |
 Thurston polyhedron:
Thurston polyhedron:QTVR (10M); POV-Ray source (2k) |
 Chazelle polyhedron:
Chazelle polyhedron:QTVR (10M); POV-Ray source (2k) |
Technical details: Rendered by POV-Ray (with image quality=4, shadows and surface colors rendered correctly but no reflections, transparency, etc). Converted to JPG by clip2gif, and to QTVR by ConvertToMovie 1.6, Make QTVR Object 1.0b4, and a simple AppleScript program for renaming POV-Ray output files to the names expected by ConvertToMovie. Views were chosen with 6 degrees of separation, decreased from QTVR's recommendation of 10 for greater smoothness of rotation. Because of the symmetry of the configuration, rendering only needed to be done through a 120 degree horizontal rotation for the Schönhardt polyhedron, and a 180 degree rotation for the other two. The Chazelle polyhedron (formed in POV-Ray as a constructive solid geometry combination of 44 halfspaces and a cube) was particularly slow to generate: each frame took roughly 12 minutes to render on a 200MHz PowerPC 603. Images were not compressed in conversion to QTVR.
From the Geometry Junkyard,
computational
and recreational geometry.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Last update: .