 Methods Based on Approximation
Methods Based on Approximation
 Methods Based on Approximation
Methods Based on Approximation
The most natural and obvious method of finding an Egyptian fraction representation for a given number is to approximate the number as closely as possible by a single unit fraction, and then to use the same method to represent the remainder. For instance, the largest unit fraction less than 5/6 is 1/2, and removing 1/2 from 5/6 leaves 1/3, so this idea leads to the representation 1/2+1/3 mentioned above. There are several ways of translating this idea into a specific algorithm.
 The Greedy Method
The Greedy Method
The greedy method produces an Egyptian fraction representation of a number q by letting the first unit fraction be the largest unit fraction less than q, and then continuing in the same manner to represent the remaining value. If q>1, we first separate out the integer part Floor[q] before representing the remaining fraction. Our implementation works by first computing a list of the fractions left after subtracting each successive term in the greedy representation, and then subtracting a shifted copy of this list from itself.
GreedyPart[q_Integer] := 0;
GreedyPart[Rational[1,y_]] := 0;
GreedyPart[q_Rational] :=
q - If[q < 0 || q > 1, Floor[q],
Rational[1,1+Quotient[1,q]]];
SubtractShifted[l_] := Drop[l,-2] - Take[l,{2,-2}];
EgyptGreedy[q_] :=
SubtractShifted[FixedPointList[GreedyPart,q]]
Let us now make sure that this routine correctly finds an Egyptian fraction representation, and analyze its performance. If we start with x/y, the remaining value after one step is (y mod x) / y(Ceiling[y/x]), which has a smaller numerator. Similarly, the numerator decreases after each further step, so the algorithm always halts. The resulting sequence of fractions clearly adds to the original input, so the only way this method could go wrong would be if two of the fractions were equal (this is not allowed in Egyptian fractions). But this can't happen, since the denominators of the fractions must be strictly increasing: if we had two successive terms 1/a and 1/b with b <= a, we could have chosen 1/(a-1) instead of 1/a.
Since the numerator decreases after each step, the number of terms in the representation of x/y is at most x. In many cases we could expect each successive numerator to be randomly distributed modulo the previous numerator; if this were really true we would instead only expect to see O(Log x) terms. The denominator is at most squared each step, so the largest denominator is at most y^(2^x) or more generally y^(2^k) where k is the number of terms. The number of operations performed by the algorithm is proportional to k, but some of these operations might involve arithmetic on very large numbers. We demonstrate this method with a simple example.
EgyptGreedy[18/23]
1 1 1 1
{-, -, --, ----}
2 4 31 2852
That example was fairly well behaved; Wagon [Wag91]suggests trying this method on 31/311, which produces a representation with 10 terms, the maximum denominator having over 500 digits. (As we will see later, other methods produce much better representations for 31/311.)
We can easily modify our code to test the assertion that the numerators of the fractions remaining at each step do indeed decrease.
EgyptGreedyNumerators[q_] :=
Numerator[Drop[FixedPointList[GreedyPart,q],-2]]
EgyptGreedyNumerators[18/23]
{18, 13, 3, 1}
 The Harmonic Method
The Harmonic Method
The greedy method treats the integer and fractional parts of a number differently. Instead, we can always remove the largest unit fraction that is smaller than both x/y and the previously removed unit fraction, even if x/y is larger than one. We treat this separately from the greedy method as it must be implemented somewhat differently FixedPointList now needs two values, the remaining fraction and the bound on the denominator. Once we have found the sequence of remaining fractions, we remove the denominator bounds by Transpose (faster than applying First to each member of the list) and subtract the shifted list from itself as before. Our function takes two arguments, the first being the number we want to represent and the second being the largest denominator already included in the representation. The same method can also be used to generate Egyptian fractions in which the first term is arbitrarily small, simply by supplying a large integer in the second argument.
HarmonicPart[{0,d_}] := {0,d};
HarmonicPart[{Rational[1,y_],d_}] := {0,d};
HarmonicPart[{q_,d_}] :=
Max[d,1+Quotient[1,q]] //
{q-1/#,#+1} &;
EgyptHarmonic[q_,d_] :=
Transpose[FixedPointList[HarmonicPart,{q,d}]][[1]] //
SubtractShifted
The algorithm constructs a fragment of the harmonic series 1/2+1/3+1/4+1/5+... until this would produce a result larger than the original input, at which point the algorithm switches to the Greedy method for the remainder. This switch must happen after at most Exp[O(x/y+Log d)] terms, because the Harmonic series diverges (the sum up to 1/k is roughly Log k). Therefore the correctness of the algorithm follows from the same analysis we saw before. However it may produce many more terms, with larger denominators, than the greedy method. Each step at most squares the denominator, so when the switch happens, the denominator of the remaining fraction can be at most doubly exponentially small with respect to x/y, and the eventual number of terms is doubly exponential in x/y (singly exponential in d). By the same analysis as the greedy algorithm, the largest denominator of the eventual representation is then at most quadruply exponential in x/y and triply exponential in d. As for the greedy method, this is only the worst case, and we can expect in practice to see one fewer level of exponentials in both the number of terms and the largest denominator. Even so, this algorithm tends to produce large representations.
EgyptHarmonic[18/23,5]
1 1 1 1 1 1 1 1
{-, -, -, -, -, --, ---, --------}
5 6 7 8 9 28 794 23010120
 The Odd Greedy Method
The Odd Greedy Method
OddGreedyPart[{0,d_}] := {0,d};
OddGreedyPart[{Rational[1,y_],d_}] := {0,d};
OddGreedyPart[{q_,d_}] :=
Max[d,1+Quotient[1,q]] //
If[OddQ[#],#,#+1] & //
{q-1/#,#+1} &;
EgyptOddGreedy[q_,d_:3] :=
Transpose[FixedPointList[OddGreedyPart,{q,d}]][[1]] //
SubtractShifted
Unlike the greedy method, the numerators of the remaining fractions do not decrease at each step. There are two reasons: first, like the harmonic method, we use a parameter d to make sure that the fractions we generate are distinct; d is used until the series 1/3+1/5+1/7+1/9+... becomes larger than q, at which point it becomes unimportant, but in this stage the numerators will in general increase. Second, whenever parity forces us to use a larger denominator than the greedy method, the denominator will again increase. We now give an example with q<1/3 to demonstrate the second phenomenon.
EgyptOddGreedyNumerators[q_,d_:3] :=
Transpose[FixedPointList[OddGreedyPart,{q,d}]][[1]] //
Numerator[Drop[#,-2]] &
EgyptOddGreedy[10/39]
1 1 1 1
{-, --, ---, ------}
5 19 265 196365
EgyptOddGreedyNumerators[10/39]
{10, 11, 14, 1}
Proving whether this method always halts remains an important open problem in the theory of Egyptian fractions [Guy81, KW91]. A heuristic argument shows that the answer is likely to be positive. After enough fractions have been generated for d to become unimportant, each step reduces the remaining fraction from some value x/y to a smaller fraction in which the numerator is between 1 and 2x-1. If each successive numerator were randomly distributed in this range, we would expect to see the numerators decrease by a factor of Exp[Integrate[Log[x],{x,0,2}]/2] ~= 0.73576 per step. Therefore we should expect the algorithm to produce roughly (Log n)/(1-Log 2) ~= 3.26 Log n unit fractions before halting, where n is the numerator of the remaining fraction at the point that d becomes unimportant. Of course nothing here is actually random, which is why this argument is not rigorous. (Also it ignores the possibility that the numerator and denominator of the fraction remaining after some steps may have a common factor, but that only serves to reduce the number of terms.) To test this argument, we compare it with the actual performance of our algorithm.
TestOddGreedy[q_] :=
EgyptOddGreedyNumerators[q] //
ListPlot[Log[#]/(1-Log[2]),
PlotJoined->True,
AxesOrigin->{0,0}]&
TestOddGreedy[1999999991/123412340001]
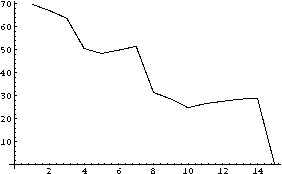
Our code normalizes the vertical axis to match our heuristic prediction of the number of steps remaining. At least for this example, the numerators seem to decrease much more quickly than our prediction, so the number of terms generated (15) is considerably smaller than the 70 we would expect. It is also interesting to note the large drops made by the numerator in the third, seventh, and final steps. A closer inspection reveals that these phenomena are due to cancellation between common factors of the numerators and denominators of intermediate terms: these three steps involve common factors of 63, 45, and 5739, and two other steps involve factors of three. It is not clear to me why such large cancellations should occur.
Egyptian Fractions, Number Theory, David Eppstein, ICS, UC Irvine