Correspondences thomasalspaugh.org/pub/fnd/correspondence.html

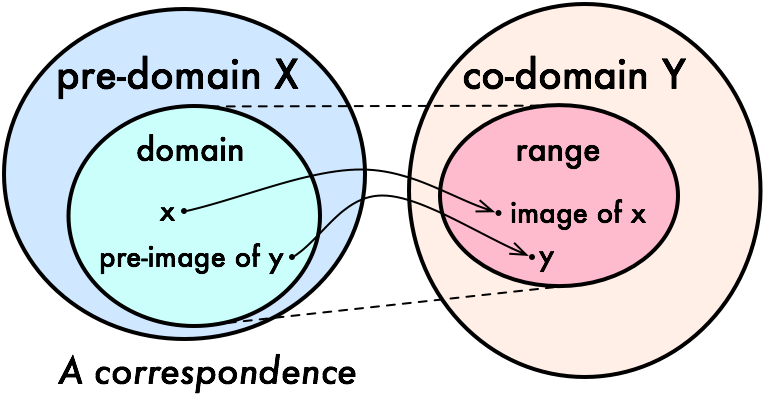
A correspondence f between X and Y is a triple (X,Y,Γ) where Γ is a subset of the Cartesian product X×Y.

The pre-domain of f is X.
The co-domain of f is Y.
Γ is the graph of f. (Note that Γ is a binary relation.)
The domain of f (written Dom(f)) is { x∈X | ∃y∈Y ( (x,y)∈Γ ) }.
The range of f (written Im(f)) is { y∈Y | ∃x∈X ( (x,y)∈Γ ) }.
y∈Y is an image of x∈X if (x,y)∈Γ.
The image of W⊆X is { y∈Y | ∃x∈W ( (x,y)∈Γ ) }.
x∈X is a pre-image of y∈Y if (y,x)∈Γ.
The pre-image of V⊆Y is { x∈X | ∃y∈V ( (x,y)∈Γ ) }.
The converse of f, written f^-1 is the correspondence whose graph is { (y,x) | (x,y)∈Γ }

Parts of a correspondence

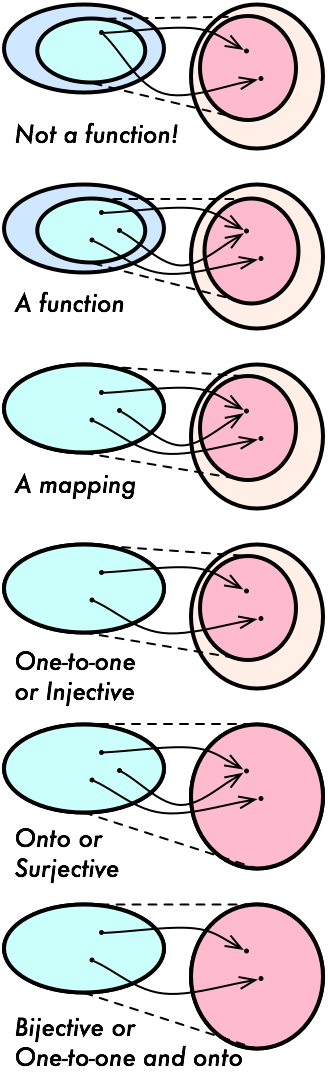
The graph of a correspondence is not constrained in the number of edges into or out of each element: the image of a domain element can be empty, a singleton, or larger,

as can the pre-image of a range element.

Functions

A function f:X→Y is a correspondence (X,Y,Γ) that assigns at most one range element to each element of its domain. Equivalently, the image of every element in the domain of f is a singleton.

Mappings

A mapping is a function whose domain is its entire pre-domain.

A mapping f:X→Y is:

onto	or	surjective	if each y∈Y has	at least	one pre-image in f
one-to-one		injective		at most
one-to-one and onto		bijective		exactly

The analogous concepts for binary relations

The pre-domain and co-domain are not relevant for a relation,, since a relation is simply a set of tuples.

A relation r that is a subset of X×Y is:

functional	if each x∈X maps to	at most one	y∈Y
injective	if each y∈Y is mapped to by	at most one	x∈X