Coloring

• Algorithms for coloring quadtrees.

• Aperiodic colored tilings, F. Gähler. Also available in postscript.

• The chromatic number of the plane. Gordon Royle and Ilan Vardi summarize what's known about the famous open problem of how many colors are needed to color the plane so that no two points at a unit distance apart get the same color. See also another article from Dave Rusin's known math pages.
  

• Coloring line arrangements. The graphs formed by overlaying a collection of lines require three, four, or five colors, depending on whether one allows three or more lines to meet at a point, and whether the lines are considered to wrap around through infinity. Stan Wagon asks similar questions for unit circle arrangements.
  

• The Four Color Theorem. A new proof by Robertson, Sanders, Seymour, and Thomas.

• Geometric graph coloring problems from "Graph Coloring Problems" by Jensen and Toft.
  

• Infect. Eric Weeks generates interesting colorings of aperiodic tilings.

• Plane color. How big can the difference between the numbers of black and white regions in a two-colored line arrangement? From Stan Wagon's PotW archive.

• Puzzles by Eric Harshbarger, mostly involving colors of and mazes on polyhedra and polyominoes.

• Rec.puzzles archive: coloring problems.

• Solution to problem 10769. Apparently problems of coloring the points of a sphere so that orthogonal points have different colors (or so that each set of coordinate basis vectors has multiple colors) has some relevance to quantum mechanics; see also papers quant-ph/9905080 and quant-ph/9911040 (on coloring just the rational points on a sphere), as well as this four-dimensional construction of an odd number of basis sets in which each vector appears an even number of times, showing that one can't color the points on a four-sphere so that each basis set has exactly one black point.

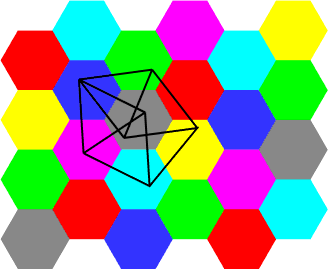
• Three-color the Penrose tiling? Mark Bickford asks if this tiling is always three-colorable. Ivars Peterson reports on a new proof by Tom Sibley and Stan Wagon that the rhomb version of the tiling is 3-colorable; A proof of 3-colorability for kites and darts was recently published by Robert Babilon [Discrete Mathematics 235(1-3):137-143, May 2001]. This is closely related to my page on line arrangement coloring, since every Penrose tiling is dual to a "multigrid", which is just an arrangement of lines in parallel families. But my page only deals with finite arrangements, while Penrose tilings are infinite.

• Three nice pentomino coloring problems, Owen Muniz.

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein, Theory Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file.