Polyominoes and Other Animals
Connected subsets of the square lattice tiling of the plane are called polyominoes. These are often classified by their number of squares, so e.g. a tetromino has four squares and a pentomino has five; this nomenclature is by analogy to the word "domino" (a shape formed by two connected squares, but unrelated in etymology to the roots for "two" or "square").If a polyomino or a higher-dimensional collection of cubes forms a shape topologically equivalent to a ball, it is called an animal. A famous open problem asks whether any animal in three dimensions can be transformed into a single cube by adding and removing cubes, at each step remaining an animal (it is known that removal alone does not always work). Other related figures include polyiamonds (collections of equilateral triangles), polyabolos (collections of half-squares), and polyhexes (collections of regular hexagons).
- Anna's pentomino page. Anna Gardberg makes pentominoes out of sculpey and agate.
- Blocking
polyominos. R. M. Kurchan asks, for each k, what is the smallest
polyomino such that k copies can form a "blocked" configuration
in which no piece can be slid free of the others, but in which any
subconfiguration is not blocked.
- Canonical
polygons.
Ronald Kyrmse investigates grid polygons in which all side lengths are
one or sqrt(2).
- Counting
polyforms, with links to images of various packing-puzzle solutions.
- Covering
the Aztec diamond with one-sided tetrasticks,
A. Wassermann.
- Dancing links.
Don Knuth discusses implementation details of polyomino search algorithms.
- A dissection puzzle. T. Sillke asks for dissections of two heptominoes into squares, and of a square into similar triangles.
- Equilateral
pentagons. Jorge Luis Mireles Jasso investigates these polygons
and dissects various polyominos into them.
- Eternity puzzle
made from "polydrafters", compounds of 30-60-90 triangles.
See also the
mathpuzzle eternity page.
- Flexagons.
Folded paper polyiamonds which can be "flexed" to show different sets of
faces. See also Harold
McIntosh's flexagon papers,
including copies of the original 1962 Conrad-Hartline papers,
also
mirrored on Erik Demaine's website.
- 4x4x4 Soma
Cube problem.
- Gerard's pentomino page.
- Golygons,
polyominoes with consecutive integer side lengths.
See also the Mathworld
Golygon page.
- Happy cubes and other three-dimensional polyomino puzzles.
- Happy Pentominoes, Vincent Goffin.
- Harary's animal game. Chris Thompson
asks about recent progress on this generalization of tic-tac-toe and
go-moku in which players place stones attempting to form certain polyominoes.
- Heesch's problem. How many times can a shape
be completely surrounded by copies of itself, without being able to tile
the entire plane? W. R. Marshall and C. Mann have recently made
significant progress on this problem using shapes formed by indenting
and outdenting the edges of polyhexes.
- Heptomino
Packings.
Clive Tooth shows us all 108 heptominos, packed into a 7x9x12 box.
- Hinged dissections of polyominoes

- Hollow
pyramid tetrasphere puzzle.
- George
Huttlin's Puzzle Page. Some ramblings in the world of polyominoes
and hexiamonds.
- Information on
Pentomino Puzzles and Information on Polyominoes, from
F. Ruskey's Combinatorial Object Server.
- Interlocking Puzzles LLC
are makers of hand crafted hardwood puzzles including burrs,
pentominoes, and polyhedra.
- Isoperimetric
polygons. Livio Zucca groups grid polygons by their perimeter
instead of by their area. For small integer perimeter the results are
just polyominos but after that it gets more complicated...
- Jacqui's
Polyomino Workshop.
Activities associated with polyominoes, aimed at the level of primary
(or elementary) school mathematics.
- Java pentomino puzzle solver, D. Eck, Hobart and William Smith Colleges.
- Iwan Jensen
counts polyominos (aka lattice animals), paths, and various related quantities.
- Kadon Enterprises,
makers of games and puzzles including polyominoes and Penrose tiles.
- Knight's Move Tessellations.
Dan Thomasson looks at tilings with polygons that can be traced out by
knight moves on a chessboard.
- Lattice
animal constant. What is the asymptotic behavior of the number
of n-square polyominos, as a function of n?
From MathSoft's favorite constants pages.
- Lego
Pentominos, Eric Harshbarger. He writes that the hard part was
finding legos in enough different colors.
See also his
Lego
math puzzles
and pentominoes
pages.
- LiveCube polycube puzzle building
toy.
- Logical art and the
art of logic, pentomino art, philosophy, and DOS software,
G. Albrecht-Buehler.
- Magazine Puzzle
Fun. Fifteen years of back issues of an Argentine magazine about
pentominoes (in English).
- The
mathematics of polyominoes, K. Gong. Counts of k-ominoes,
Macintosh polyomino software, and more links.
- Maximum convex hulls of connected systems of segments and of polyominoes. Bezdek, Brass, and Harborth place bounds on the convex area needed to contain a polyomino.
- The MindBlock.
Reassemble a chessboard cut into twelve interlocking polyominos.
- A minimal
domino tiling. How small a square board can one fill with dominos in
a way that can't be separated into two smaller rectangles?
From Stan Wagon's
PotW archive.
- Miscellaneous
polyomino explorations. Alexandre Owen Muniz
looks at double polyomino tilings that simultaneously cover all
half-grid edges, magic polyominoes, and more.
- Odd rectangles for L4n+2.
Phillippe Rosselet shows that any L-shaped (4n+2)-omino can tile a rectangle
with an odd side.
- Packing Ferrers Shapes.
Alon, Bóna, and Spencer show that one can't cover very much of an n by p(n)
rectangle with staircase polyominoes (where p(n) is the number of these
shapes).
- Packing
polyominoes.
Mark Michell investigates the problem of arranging pentominoes into
rectangles of various (non-integer) aspect ratios,
in order to saw the largest possible pieces from a given size piece of
wood.
- Pairwise
touching hypercubes. Erich Friedman asks how to partition the unit cubes
of an a*b*c-unit rectangular box into as many connected polycubes as
possible with a shared face between every pair of polycubes.
He lists both general upper and lower bounds as functions of a, b, and
c, and specific constructions for specific sizes of box.
I've seen the same question asked for d-dimensional hypercubes
formed out of 2^d unit hypercubes; there is a lower bound of roughly
2d/2 (from embedding a 2*2d/2*2d/2 box
into the hypercube)
and an upper bound of O(2d/2 sqrt d)
(from computing how many cubes must be in a polycube
to give it enough faces to touch all the others).
- Pentamini.
Italian site on pentominoes, by L. Zucca.
- Pentomino.
Extensive website on polyomino problems, developed by secondary school
students in Belgium. Includes regular prize contest problems involving
maximizing the area enclosed by polyominos in various ways.
- The Pentomino
Dictionary and other oulipian exercises,
G. Esposito-Farèse. The twelve pentominoes
resemble letters; what words do they spell? Also includes sections on
"perecquian" configurations and a pentomino jigsaw puzzle.
- Pentomino
dissection of a square annulus. From Scott Kim's Inversions Gallery.
- Pentomino
project-of-the-month from the Geometry Forum. List the pentominoes;
fold them to form a cube; play a pentomino game.
See also proteon's polyomino cube-unfoldings and
Livio
Zucca's polyomino-covered cube.
- Pento - A
Program to Solve the Pentominoes Problem. Sean Vyain.
- Pento
pentomino solving software from Amamas Software.
- Pentomino HungarIQa.
What happens to standard pentomino puzzles and games
if you use poly-rhombs instead of poly-squares?
- Pentomino
relationships.
A. Smith classifies pentomino packings according to their shared
subpatterns.
- Pentominoes,
expository paper by R. Bhat and A. Fletcher.
- Pentominoes - an introduction.
From the Centre for Innovation in Mathematics Teaching.
- Lorente Philippe's pentomino homepage. In French.
- The Poly Pages.
Andrew L. Clarke provides information and links on the various polyforms.
- PolyB
Unix software for enumerating lattice animals, Paul Janssens.
- Polygon Puzzle
open source polyomino and polyform placement solitaire game.
- Polyform and dissection puzzle links.
- Polyforms.
Ed Pegg Jr.'s site has many pages on tiling, packing, and related problems
involving polyominos, polyiamonds, polyspheres, and related shapes.
- Polyform
spirals.
- Polyiamond
exclusion. Colonel Sicherman asks what fraction of the triangles
need to be removed from a regular triangular tiling of the plane, in
order to make sure that the remaining triangles contain no copy of a
given polyiamond.
- Polyiamonds.
This Geometry Forum problem of the week asks whether a six-point star
can be dissected to form eight distinct hexiamonds.
- Polyomino
applet, Wil Laan.
- Polyomino covers.
Alexandre Owen Muniz investigates the minimum size of a polygon that can
contain each of the n-ominoes.
- Polyomino
enumeration, K. S. Brown.
- Polyomino inclusion problem.
Yann David wants to know how to test whether all sufficiently large
polyominoes contain at least one member of a given set.
- Polyomino
problems and variations of a theme. Information about filling
rectangles, other polygons, boxes, etc., with dominoes, trominoes,
tetrominoes, pentominoes, solid pentominoes, hexiamonds, and whatever
else people have invented as variations of a theme.
- Polyomino tiling.
Joseph Myers classifies the n-ominoes up to n=15 according to how
symmetrically they can tile the plane.
- Polyominoes
7.0 Macintosh shareware.
- Polyominoids,
connected sets of squares in a 3d cubical lattice.
Includes a Java applet as well as non-animated description.
By Jorge L. Mireles Jasso.
- Polypolygon
tilings, S. Dutch.
- Primes
of a 14-omino. Michael Reid shows that a 3x6 rectangle with a 2x2
bite removed can tile a (much larger) rectangle.
It is open whether it can do this using an odd number of copies.
- Prolog soma-cube puzzle program
- Proteon's Puzzle Notes
Wen-Shan Kao covers cubes with polyominos and polysticks, packs worms
into boxes, and studies giant tangram like puzzles.
- Puzzle Fun,
a quarterly bulletin edited by R. Kurchan about polyominoes and
other puzzles.
- Puzzles
by Eric Harshbarger, mostly involving colors of and mazes on
polyhedra and polyominoes.
- Puzzling
paper folding. An amusing origami polyabolo eversion puzzle.
- Random domino tiling of an Aztec diamond
and other undergrad research on random tiling.
- Reproduction of
sexehexes. Livio Zucca finds an interesting fractal polyhex based on
a simple matching rule.
- Rujith de Silva's
pentomino applet.
- A simple dodecahedron tiling puzzle.
Cover the dodecahedron's faces with pentagonal tetrominos.
- A small puzzle.
Joe Fields asks whether a certain decomposition into L-shaped
polyominoes provides a universal solution to dissections of pythagorean
triples of squares.
- Solution
to the pentomino problem by pete@bignode.equinox.gen.nz, from the
rec.puzzles archives.
- Soma cube
applet.
- The soma cube page and pentomino page, J. Jenicek.
- sqfig and sqtile,
software by Eric Laroche for generating polyominoes and polyomino
tilings.
- Square Knots. This article by Brian Hayes for American Scientist
examines how likely it is that a random
lattice polygon is knotted.
- Tesselating
locking polyominos, Bob Newman.
- This
is your brain on Tetris. Are pentominos really "an ancient Roman
puzzle"?
- The
three dimensional polyominoes of minimal area, L. Alonso and
R. Cert, Elect. J. Combinatorics.
- Three
nice pentomino coloring problems, Owen Muniz.
- A
tiling from ell. Stan Wagon asks
which rectangles can be tiled with an ell-tromino.
- Tiling the infinite grid with finite clusters.
Mario Szegedy describes an algorithm for determining whether a (possibly
disconnected) polyomino will tile the plane by translation,
in the case where the number of squares in the polyomino is a prime
or four.
- The tiling puzzle games of
OOG. Windows and Java software for tangrams, polyominoes, and polyhexes.
- Tiling rectangles
and half strips with congruent polyominoes, and
Tiling a square with eight congruent polyominoes, Michael Reid.
- Tiling
stuff. J. L. King examines problems of determining whether a given
rectangular brick can be tiled by certain smaller bricks.
- Tiling with four cubes.
Torsten Sillke summarizes results and conjectures on
the problem of tiling 3-dimensional boxes with a tile
formed by gluing three cubes onto three adjacent faces
of a fourth cube.
- Tiling with
notched cubes. Robert Hochberg and Michael Reid exhibit an unboxable
reptile: a polycube that can tile a larger copy of itself, but can't
tile any rectangular block.
- Tiling with polyominos.
Michael Reid summarizes results on the ability to cover
rectangles and other figures using polyominoes. See also
Torsten
Sillke's page of results on similar problems.
- Tilings.
Lecture notes from the Clay Math Institute, by Richard Stanley and
Federico Ardila, discussing polyomino tilings, coloring arguments for
proving the nonexistence of tilings, counting how many tilings a region
has, the arctic circle theorem for domino tilings of diamonds,
tiling the unit square with unit-fraction rectangles, symmetry groups,
penrose tilings, and more. In only 21 pages, including the annotated
bibliography. A nice but necessarily concise introduction to the subject.
(Via Andrei Lopatenko.)
- Triangular
polyhex tilings. What is the smallest equilateral triangle that can
be tiled by a given polyhex?
- Unbalanced
anisohedral tiling.
Joseph Myers and
John Berglund find a polyhex that must be placed two different ways in
a tiling of a plane, such that one placement occurs twice as often as
the other.
- Unbeatable Tetris.
Java demonstration that this tetromino-packing game is a forced win
for the side dealing the tetrominoes.
- Unfolding
the tesseract. Peter Turney lists the 261 polycubes that can be
folded in four dimensions to form the surface of a hypercube,
and provides animations of the unfolding process.
- Variations
on the theme of polyominos.
- When
can a polygon fold to a polytope? A. Lubiw and J. O'Rourke describe
algorithms for finding the folds that turn an unfolded paper model of a
polyhedron into the polyhedron itself. It turns out that the familiar
cross hexomino pattern for folding cubes can also be used to fold three other
polyhedra with four, five, and eight sides.
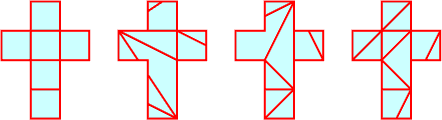
- A word problem.
Group theoretic mathematics for determining whether a polygon formed out
of hexagons can be dissected into three-hexagon triangles,
or whether a polygon formed out of squares can be dissected
into restricted-orientation triominoes.
- Xominoes.
Livio Zucca finds a set of markings for the edges of a square that lead
to exactly 100 possible tiles, and asks how to fit them into a 10x10 grid.
- Zillions
of Games: Pento.