Planar Geometry

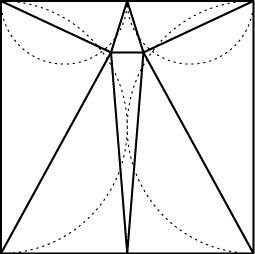
• Acute square triangulation. Can one partition the square into triangles with all angles acute? How many triangles are needed, and what is the best angle bound possible?
  

• Adventitious geometry. Quadrilaterals in which the sides and diagonals form more rational angles with each other than one might expect. Dave Rusin's known math pages include another article on the same problem.

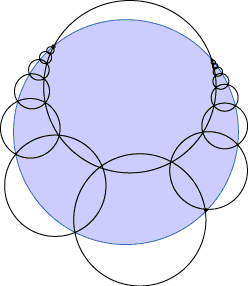
• 1st and 2nd Ajima-Malfatti points. How to pack three circles in a triangle so they each touch the other two and two triangle sides. This problem has a curious history, described in Wells' Penguin Dictionary of Curious and Interesting Geometry: Malfatti's original (1803) question was to carve three columns out of a prism-shaped block of marble with as little wasted stone as possible, but it wasn't until 1967 that it was shown that these three mutually tangent circles are never the right answer. See also this Cabri geometry page, the MathWorld Malfatti circles page, and the Wikipedia Malfatti circles page.

• Are all triangles isosceles? A fallacious proof from K. S. Brown's math pages.

• Ancient Islamic Penrose Tiles. Peter Lu uncovers evidence that the architects of a 500-year-old Iranian shrine used Penrose tiling to lay out the decorative patterns on its archways. From Ivars Peterson's MathTrek.

• Angle trisection, from the geometry forum archives.

• Animated proof of the Pythagorean theorem, M. D. Meyerson, US Naval Academy.

• Aperiodic colored tilings, F. Gähler. Also available in postscript.

• Aperiodic tiling and Penrose tiles, Steve Edwards.

• Apollonian Gasket, a fractal circle packing formed by packing smaller circles into each triangular gap formed by three larger circles. From MathWorld.

• Applications of shapes of constant width. A Reuleaux triangle doesn't quite drill out a square hole (it leaves rounded corners) but a different and less-symmetric constant-width shape based on an isosceles right triangle can be used to do so. This web page also discusses coin design, cams, and rotary engines, all based on curves of constant width; see also discussion on Metafilter.

• Arc length surprise. The sum of the areas of the regions between a circular arc and the x-axis, and between the arc and the y-axis, does not depend on the position of the arc! From Mudd Math Fun Facts.

• Area of the Mandelbrot set. One can upper bound this area by filling the area around the set by disks, or lower bound it by counting pixels; strangely, Stan Isaacs notes, these two methods do not seem to give the same answer.

• On the average height of jute crops in the month of September. Vijay Raghavan points out an obscure reference to average case analysis of the Euclidean traveling salesman problem.

• David Bailey's world of tesselations. Primarily consists of Escher-like drawings but also includes an interesting section about Kepler's work on polyhedra.

• Balanced ternary reptiles, Cantor's hourglass reptile, spiral reptile, stretchtiles, trisection of India, the three Bodhi problem, and other Fractal tilings by R. W. Gosper.

• Belousov's Brew. A recipe for making spiraling patterns in chemical reactions.

• BitArt spirolateral gallery (requires JavaScript to view large images, and Java to view self-running demo or construct new spirolaterals).

• Brahmagupta's formula. A "Heron-type" formula for the maximum area of a quadrilateral, Col. Sicherman's fave. He asks if it has higher-dimensional generalizations.

• Buffon's needle. What is the probability that a dropped needle lands on a crack on a hardwood floor? From Kunkel's mathematics lessons.

• Building a better beam detector. This is a set that intersects all lines through the unit disk. The construction below achieves total length approximately 5.1547, but better bounds were previously known.
  

• Carnival triangles. A factoid about similar triangles inspired by a trigonometric identity.

• Centers of maximum matchings. Andy Fingerhut asks, given a maximum (not minimum) matching of six points in the Euclidean plane, whether there is a center point close to all matched edges (within distance a constant times the length of the edge). If so, it could be extended to more points via Helly's theorem. Apparently this is related to communication network design. I include a response I sent with a proof (of a constant worse than the one he wanted, but generalizing as well to bipartite matching).

• Chaotic tiling of two kinds of equilateral pentagon, with 30degree symmetry, Ed Pegg Jr.

• The chromatic number of the plane. Gordon Royle and Ilan Vardi summarize what's known about the famous open problem of how many colors are needed to color the plane so that no two points at a unit distance apart get the same color. See also another article from Dave Rusin's known math pages.
  

• Circle packing and discrete complex analysis. Research by Ken Stephenson including pictures, a bibliography, and downloadable circle packing software.

• Circle packings. Gareth McCaughan describes the connection between collections of tangent circles and conformal mapping. Includes some pretty postscript packing pictures.

• Circles in ellipses. James Buddenhagen asks for the smallest ellipse that contains two disjoint unit circles. Discussion continued in a thread on three circles in an ellipse.
  

• Circular coverage constants. How big must N equal disks be in order to completely cover the unit disk? What about disks with sizes in geometric progression? From MathSoft's favorite constants pages.
  

• Circular quadrilaterals. Bill Taylor notes that if one connects the opposite midpoints of a partition of the circle into four chords, the two line segments you get are at right angles. Geoff Bailey supplies an elegant proof.

• Circumcenters of triangles. Joe O'Rourke, Dave Watson, and William Flis compare formulas for computing the coordinates of a circle's center from three boundary points, and higher dimensional generalizations.

• Circumference/perimeter of an ellipse: formula(s). Interesting and detailed survey of formulas giving accurate approximations to this value, which can not be expressed exactly as a closed form formula.

• Coloring line arrangements. The graphs formed by overlaying a collection of lines require three, four, or five colors, depending on whether one allows three or more lines to meet at a point, and whether the lines are considered to wrap around through infinity. Stan Wagon asks similar questions for unit circle arrangements.
  

• Complex regular tesselations on the Euclid plane, Hironori Sakamoto.

• a computational approach to tilings. Daniel Huson investigates the combinatorics of periodic tilings in two and three dimensions, including a classification of the tilings by shapes topologically equivalent to the five Platonic solids.

• Contour plots with trig functions. Eric Weeks discovers a method of making interesting non-moiré patterns.

• Cool math: tessellations

• Covering points by rectangles. Stan Shebs discusses the problem of finding a minimum number of copies of a given rectangle that will cover all points in some set, and mentions an application to a computer strategy game. This is NP-hard, but I don't know how easy it is to approximate; most related work I know of is on optimizing the rectangle size for a cover by a fixed number of rectangles.

• The Curlicue Fractal, Fergus C. Murray.

• Curvature of crossing convex curves. Oded Schramm considers two smooth convex planar curves crossing at at least three points, and claims that the minimum curvature of one is at most the maximum curvature of the other. Apparently this is related to conformal mapping. He asks for prior appearances of this problem in the literature.

• Delaunay and regular triangulations. Lecture by Herbert Edelsbrunner, transcribed by Pedro Ramos and Saugata Basu. The regular triangulation has been popularized by Herbert as the appropriate generalization of the Delaunay triangulation to collections of disks.

• Delaunay triangulation and points of intersection of lines. Tom McGlynn asks whether the DT of a line arrangement's vertices must respect the lines; H. K. Ruud shows that the answer is no.

• Dilation-free planar graphs. How can you arrange n points so that the set of all lines between them forms a planar graph with no extra vertices?
  

• Disjoint triangles. Any 3n points in the plane can be partitioned into n disjoint triangles. A. Bogomolny gives a simple proof and discusses some generalizations.

• Dissection challenges. Joshua Bao asks for some dissections of squares into other figures.
  

• Dissection and dissection tiling. This page describes problems of partitioning polygons into pieces that can be rearranged to tile the plane. (With references to publications on dissection.)
  

• Dissection problem-of-the-month from the Geometry Forum. Cut squares and equilateral triangles into pieces and rearrange them to form each other or smaller copies of themselves.

• Distinct point set with the same distance multiset. From K. S. Brown's Math Pages.

• DUST software for visualization of Voronoi diagrams, Delaunay triangulations, minimum spanning trees, and matchings, U. Köln.

• Dynamic formation of Poisson-Voronoi tiles. David Griffeath constructs Voronoi diagrams using cellular automata.

• The Dynamic Systems and Technology Project at Boston Univ. offers several Java applets and animations of fractals and iterated function systems.

• An eight-point arrangement in which each perpendicular bisector passes through two other points. From Stan Wagon's PotW archive.

• Ellipse game, or whack-a-focus.

• Elliptical billiard tables, H. Serras, Ghent.

• Enumeration of polygon triangulations and other combinatorial representations of the Catalan numbers.

• Equiangular spiral. Properties of Bernoulli's logarithmic 'spiralis mirabilis'.

• An equilateral dillemma. IBM asks you to prove that the only triangles that can be circumscribed around an equilateral triangle, with their vertices equidistant from the equilateral vertices, are themselves equilateral.

• Equilateral pentagons. Jorge Luis Mireles Jasso investigates these polygons and dissects various polyominos into them.

• Equilateral pentagons that tile the plane, Livio Zucca.

• Equilateral triangles. Dan Asimov asks how large a triangle will fit into a square torus; equivalently, the densest packing of equilateral triangles in the pattern of a square lattice. There is only one parameter to optimize, the angle of the triangle to the lattice vectors; my answer is that the densest packing occurs when this angle is 15 or 45 degrees, shown below. (If the lattice doesn't have to be square, it is possible to get density 2/3; apparently this was long known, e.g. see Fáry, Bull. Soc. Math. France 78 (1950) 152.)

  Asimov also asks for the smallest triangle that will always cover at least one point of the integer lattice, or equivalently a triangle such that no matter at what angle you place copies of it on an integer lattice, they always cover the plane; my guess is that the worst angle is parallel and 30 degrees to the lattice, giving a triangle with 2-unit sides and contradicting an earlier answer to Asimov's question.

  

• Equivalents of the parallel postulate. David Wilson quotes a book by George Martin, listing 26 axioms equivalent to Euclid's parallel postulate. See also Scott Brodie's proof of equivalence with the Pythagorean theorem.

• Erich's Packing Page. Erich Friedman enjoys packing geometric shapes into other geometric shapes.

• An extension of Napoleon's theorem. Placing similar isosceles triangles on the sides of an affine-transformed regular polygon results in a figure where the triangle vertices lie on another regular polygon. Geometer's sketchpad animation by John Berglund.

• Fagnano's problem of inscribing a minimum-perimeter triangle within another triangle, animated in Java by A. Bogomolny. See also part II, part III, and a reversed version.

• Fagnano's theorem. This involves differences of lengths in an ellipse. Joe Keane asks why it is unusual.

• Famous curve applet index. Over fifty well-known plane curves, animated as Java applets.

• Fermat's spiral and the line between Yin and Yang. Taras Banakh, Oleg Verbitsky, and Yaroslav Vorobets argue that the ideal shape of the dividing line in a Yin-Yang symbol is formed, not from two semicircles, but from Fermat's spiral.

• Finding the wood by the trees. Marc van Kreveld studies strategies by which a blind man with a rope could map out a forest.

• Five circle theorem. Karl Rubin and Noam Elkies asked for a proof that a certain construction leads to five cocircular points. This result was subsequently discovered by Allan Adler and Gerald Edgar to be essentially the same as a theorem proven in 1939 by F. Bath.

• Flatland: A Romance of Many Dimensions.

• The Four Color Theorem. A new proof by Robertson, Sanders, Seymour, and Thomas.

• Fractal bacteria.

• A fractal beta-skeleton with high dilation. Beta-skeletons are graphs used, among other applications, in predicting which pairs of cities should be connected by roads in a road network. But if you build your road network this way, it may take you a long time to get from point a to point b.
  

• Fractal instances of the traveling salesman problem, P. Moscato, Buenos Aires.

• Fractal knots, Robert Fathauer.

• Fractal patterns formed by repeated inversion of circles: Indra's Pearls Inversion graphics gallery, Xah Lee. Inversive circles, W. Gilbert, Waterloo.
  

• Erich Friedman's dissection puzzle. Partition a 21x42x42 isosceles triangles into six smaller triangles, all similar to the original but with no two equal sizes. (The link is to a drawing of the solution.)

• Gauss' tomb. The story that he asked for (and failed to get) a regular 17-gon carved on it leads to some discussion of 17-gon construction and perfectly scalene triangles.

• Gaussian continued fractions. Stephen Fortescue discusses some connections between basic number-theoretic algorithms and the geometry of tilings of 2d and 3d hyperbolic spaces.

• Generating Fractals from Voronoi Diagrams, Ken Shirriff, Berkeley and Sun.

• Geometric Dissections by Gavin Theobald.

• Geometry, algebra, and the analysis of polygons. Notes by M. Brundage on a talk by B. Grünbaum on vector spaces formed by planar n-gons under componentwise addition.

• Geometry corner with Martin Gardner. He describes some problems of cutting polygons into similar and congruent parts. From the MAT 007 I News.

• Ghost diagrams, Paul Harrison's software for finding tilings with Wang-tile-like hexagonal tiles, specified by matching rules on their edges. These systems are Turing-complete, so capable of forming all sorts of complex patterns; the web site shows binary circuitry, fractals, 1d cellular automaton simulation, Feynman diagrams, and more.

• Graham's hexagon, maximizing the ratio of area to diameter. You'd expect it to be a regular hexagon, right? Wrong. From MathSoft's favorite constants pages. See also Wolfgang Schildbach's java animation of this hexagon and similar n-gons for larger values of n.

• Greg's favorite math party trick. A nice visual proof of van Aubel's theorem, that equal perpendicular line segments connect the opposite centers of squares exterior to the sides of any quadrilateral. See also Wikipedia, MathWorld, Geometry from the land of the Incas, interactive Java applet.

• Heilbronn triangle constants. How can you place n points in a square so that all triangles formed by triples of points have large area?

• Hero's Formula for the area of a triangle in terms of its side lengths. Mark Dominus explains.

• How many intersection points can you form from an n-line arrangement? Equivalently, how many opposite pairs of faces can an n-zone zonohedron have? It must be a number between n-1 and n(n-1)/2, but not all of those values are possible.

• How many points can one find in three-dimensional space so that all triangles are equilateral or isosceles? One eight-point solution is formed by placing three points on the axis of a regular pentagon. This problem seems related to the fact that any planar point set forms O(n^7/3) isosceles triangles; in three dimensions, Theta(n³) are possible (by generalizing the pentagon solution above). From Stan Wagon's PotW archive.

• How to construct a golden rectangle, K. Wiedman.

• Hyperbolic games. Freeware multiplatform software for games such as Sudoku on hyperbolic surfaces, intended as a way for students to gain familiarity with hyperbolic geometry. By Jeff Weeks.

• In plane sight. Equilateral triangle visibility problem from Andy Drucker. See also here.

• Infect. Eric Weeks generates interesting colorings of aperiodic tilings.

• Infinite families of simplicial arrangements.
  

• Integer distances. Robert Israel gives a nice proof (originally due to Erdös) of the fact that, in any non-colinear planar point set in which all distances are integers, there are only finitely many points. Infinite sets of points with rational distances are known, from which arbitrarily large finite sets of points with integer distances can be constructed; however it is open whether there are even seven points at integer distances in general position (no three in a line and no four on a circle).

• Interactive Delaunay triangulation and Voronoi diagrams:
  VoroGlide, Icking, Klein, Köllner, Ma, Hagen.
  D. Watson, CSIRO, Australia.
  Baker et al., Brown U.
  Paul Chew, Cornell U.
  

• Interconnection Trees. Java minimum spanning tree implementation, Joe Ganley, Virginia.

• Inversive geometry. Geometric transformations of circles, animated with CabriJava.

• Irreptiles. Karl Scherer and Erich Friedman generalize the concept of a reptile (tiling of a shape by smaller copies of itself) to allow the copies to have different scales. See also Karl Scherer's two-part irreptile puzzle.
  

• Islamic geometric art.

• Isoperimetric polygons. Livio Zucca groups grid polygons by their perimeter instead of by their area. For small integer perimeter the results are just polyominos but after that it gets more complicated...

• The isoperimetric problem for pinwheel tilings. In these aperiodic tilings (generated by a substitution system involving similar triangles) vertices are connected by paths almost as good as the Euclidean straight-line distance.

• Isosceles pairs. Stan Wagon asks which triangles can be dissected into two isosceles triangles.

• Isotiles, workbook on the shapes that can be formed by combining isosceles triangles with side lengths in the golden ratio.

• Japanese Triangulation Theorem. The sum of inradii in a triangulation of a cyclic polygon doesn't depend on which triangulation you choose! Conversely, any polygon for which this is true is cyclic.

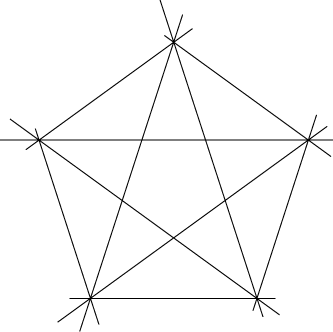
• Jiang Zhe-Ming's geometry challenge. A pretty problem involving cocircularity of five points defined by circles around a pentagram.

• Jordan sorting. This is the problem of sorting (by x-coordinate) the intersections of a line with a simple polygon. Complicated linear time algorithms for this are known (for instance one can triangulate the polygon then walk from triangle to triangle); Paul Callahan discusses an alternate algorithm based on the dynamic optimality conjecture for splay trees.

• Kabon Triangles. How many disjoint triangles can you make out of n line segments? From Eric Weisstein's treasure trove of mathematics. According to Toshi Kato, these should actually be called Kobon triangles, after Kobon Fujimura in Japan; Kato also tells me that Mr. Saburo Tamura proved a bound of F(n) <n(n-2)/3.
  

• The Kakeya-Besicovitch problem. Paul Wellin describes this famous problem of rotating a needle in a planar set of minimal area. As it turns out the area can be made arbitrarily close to zero. See also Steven Finch's page on Kakeya-Besicovitch constants, and Eric Weisstein's page on the Kakeya Needle Problem.

• Kaleidoscope geometry, Ephraim Fithian.

• Kaleidotile software for visualizing tilings of the sphere, Euclidean plane, and hyperbolic plane.

• Kali, software for making symmetrical drawings based on any of the 17 plane tiling groups.

• kD-tree demo. Java applet by Jacob Marner.

• Richard Kenyon's Gallery of tilings by squares and equilateral triangles of varying sizes.

• The Kneser-Poulsen Conjecture. Bezdek and Connelly solve an old problem about pushing disks together.

• Labyrinth tiling. This aperiodic substitution tiling by equilateral and isosceles triangles forms fractal space-filling labyrinths.
  

• Largest 5-gon in a square, or more interestingly smallest equilateral pentagon inscribed in a square. Posting to sci.math by Rainer Rosenthal.

• Layered graph drawing.
  

• Lego sextic. Clive Tooth draws infinity symbols using lego linkages, and analyzes the resulting algebraic variety.

• Lenses, rational-angled equilateral hexagons can tile the plane in various interesting patterns. See also Jorge Mireles' nice lens puzzle applet: rotate decagons and stars to get the pieces into the right places.

• LightSource sacred geometry software.

• Line designs for the computer. Jill Britton brings to the web material from John Millington's 1989 book on geometric patterns formed by stitching yarn through cardboard. The Java simulation of a Spectrum computer running Basic programs is a little (ok a lot) clunky, and froze Mozilla when I tried it, but there's also plenty of interesting static content.

• Log-spiral tiling, and other radial and spiral tilings, S. Dutch.

• Looking at sunflowers. In this abstract of an undergraduate research paper, Surat Intasang investigates the spiral patterns formed by sunflower seeds, and discovers that often four sets of spirals can be discerned, rather than the two sets one normally notices.

• A map of all triangles and the search for the ideal acute scalene triangle, Robert Simms.

• The Margulis Napkin Problem. Jim Propp asked for a proof that the perimeter of a flat origami figure must be at most that of the original starting square. Gregory Sorkin provides a simple example showing that on the contrary, the perimeter can be arbitrarily large.

• Marius Fine Art Studio Sacred Geometry Art. Prints and paintings for sale of various geometric designs.

• Match sticks in the summer. Ivars Peterson discusses the graphs that can be formed by connecting vertices by non-crossing equal-length line segments.

• Midpoint triangle porism. Two nested circles define a continuous family of triangles having endpoints on the outer circle and edge midpoints on the inner circle. A similar porism works for quadrilaterals and, seemingly, higher order polygons. Geometer's sketchpad animations by John Berglund.

• Minimize the slopes. How few different slopes can be formed by the lines connecting 881 points? From Stan Wagon's PotW archive.

• Miquel's pentagram theorem on circles associated with a pentagon. With annoying music.

• Mirrored room illumination. A summary by Christine Piatko of the old open problem of, given a polygon in which all sides are perfect mirrors, and a point source of light, whether the entire polygon will be lit up. The answer is no if smooth curves are allowed. See also Eric Weisstein's page on the Illumination Problem.

• Moebius transformations revealed. Video by Douglas N. Arnold and Jonathan Rogness explaining 2d Moebius transformations in terms of the motions of a 3d sphere. See also MathTrek.

• Monge's theorem and Desargues' theorem, identified. Thomas Banchoff relates these two results, on colinearity of intersections of external tangents to disjoint circles, and of intersections of sides of perspective triangles, respectively. He also describes generalizations to higher dimensional spheres.

• Moser's Worm. What is the smallest area shape (in a given class of shapes) that can cover any unit-length path? Part of Mathsoft's collection of mathematical constants.

• Natural neighbors. Dave Watson supplies instances where shapes from nature are (almost) Voronoi polygons. He also has a page of related references.

• The no-three-in-line problem. How many points can be placed in an n*n grid with no three on a common line? The solution is known to be between 1.5n and 2n. Achim Flammenkamp discusses some new computational results including bounds on the number of symmetric solutions.

• Non-Euclidean geometry with LOGO. A project at Cardiff, Wales, for using the LOGO programming language to help mathematics students visualise non-Euclidean geometry.

• Occurrence of the conics. Jill Britton explains how the different conic curves can all be formed by slicing the same cone at different angles, and finds many examples of them in technology and nature.

• Origami: a study in symmetry. M. Johnson and B. Beug, Capital H.S.

• Packing circles in circles and circles on a sphere, Jim Buddenhagen. Mostly about optimal packing but includes also some nonoptimal spiral and pinwheel packings.

• Packing pennies in the plane, an illustrated proof of Kepler's conjecture in 2D by Bill Casselman.

• Packing results, D. Boll. C code for finding dense packings of circles in circles, circles in squares, and spheres in spheres.

• Packomania!

• A pair of triangle centers, Vincent Goffin. Do these really count as centers? They are invariant under translation and rotation but switch places under reflection.

• Paper folding a 30-60-90 triangle. From the geometry.puzzles archives.

• Paperfolding and the dragon curve. David Wright discusses the connections between the dragon fractal, symbolic dynamics, folded pieces of paper, and trigonometric sums.

• Penrose tilings. This five-fold-symmetric tiling by rhombs or kites and darts is probably the most well known aperiodic tiling.

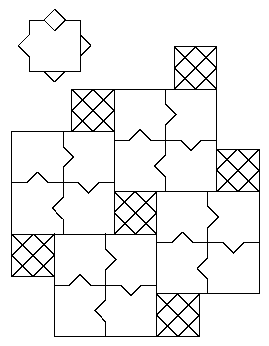
• Pentagonal Tessellations. John Savard experiments with substitution systems to produce tilings resembling Kepler's.

• Pentagons that tile the plane, Bob Jenkins. See also Ed Pegg's page on pentagon tiles.

• The pentagram and the golden ratio. Thomas Green, Contra Costa College.

• Perron Number Tiling Systems. Mathematica software for computing fractals that tile the plane from Perron numbers.

• Person polygons. Marc van Kreveld defines this interesting and important class of simple polygons, and derives a linear time algorithm (with a rather large constant factor) for recognizing a special case in which there are many reflex vertices.

• The Perspective Page. A short introduction to the geometry of perspective drawing.

• Pick's Theorem. Mark Dominus explains the formula for area of polygons with vertices in an integer grid.

• Pictures of various spirals, Eric Weeks.

• Place kicking locus in rugby, Michael de Villiers. See also Villiers' other geometry papers.

• Plan for pocket-machining Austria, M. Held, Salzburg.

• Plane color. How big can the difference between the numbers of black and white regions in a two-colored line arrangement? From Stan Wagon's PotW archive.

• Plates and crowns. Erich Friedman investigates the convex polygons that can be dissected into certain pentagons and heptagons having all angles right or 135 degrees.

• Polygons with angles of different k-gons. Leroy Quet asks whether polygons formed by combining the angles of different regular polygons can tile the plane. The answer turns out to be related to Egyptian fraction decompositions of 1 and 1/2.

• Polyhedral nets and dissection. David Paterson outlines an algorithm to search for minimal dissections.

• Polyominoes, figures formed from subsets of the square lattice tiling of the plane. Interesting problems associated with these shapes include finding all of them, determining which ones tile the plane, and dissecting rectangles or other shapes into sets of them. Also includes related material on polyiamonds, polyhexes, and animals.

• Poncelet's porism, the theorem that if a polygon is simultaneously inscribed in one circle and circumscribed in another, then there exists an infinite family of such polygons, one touching each point of each circle. From the secret blogging seminar.

• Popsicle stick bombs, lashings and weavings in the plane, F. Saliola.

• Postscript geometry. Bill Casselman uses postscript to motivate a course in Euclidean geometry. See also his Coxeter group graph paper, and Ed Rosten's postscript doodles. Beware, however, that postscript can not really represent such basic geometric primitives as circles, instead approximating them by splines.

• A pre-sliced triangle. Given a triangle with three lines drawn across it, how to draw more lines to make it into a triangulation? From Stan Wagon's PotW archive.

• Projective Duality. This Java applet by F. Henle of Dartmouth demonstrates three different incidence-preserving translations from points to lines and vice versa in the projective plane.

• Proofs of the Pythagorean Theorem.

• Pythagoras' Haven. Java animation of Euclid's proof of the Pythagorean theorem.

• Pythagorean theorem by dissection, part II, and part III, Java Applets by A. Bogomolny.

• Pythagorean tilings. William Heierman asks about dissections of rectangles into dissimilar integer-sided right triangles.

• Random spherical arc crossings. Bill Taylor and Tal Kubo prove that if one takes two random geodesics on the sphere, the probability that they cross is 1/8. This seems closely related a famous problem on the probability of choosing a convex quadrilateral from a planar distribution. The minimum (over all possible distributions) of this probability also turns out to solve a seemingly unrelated combinatorial geometry problem, on the minimum number of crossings possible in a drawing of the complete graph with straight-line edges: see also "The rectilinear crossing number of a complete graph and Sylvester's four point problem of geometric probability", E. Scheinerman and H. Wilf, Amer. Math. Monthly 101 (1994) 939-943, rectilinear crossing constant, S. Finch, MathSoft, and Calluna's pit, Douglas Reay.

• Random polygons. Tim Lambert summarizes responses to a request for a good random distribution on the n-vertex simple polygons.

• Rational square. David Turner shows that a rectangle can only be dissected into finitely many squares if its sides are in a rational proportion.

• Rational triangles. This well known problem asks whether there exists a triangle with the side lengths, medians, altitudes, and area all rational numbers. Randall Rathbun provides some "near misses" -- triangles in which most but not all of these quantities are irrational. See also Dan Asimov's question in geometry.puzzles about integer right-angled tetrahedra.

• Rec.puzzles archive: dissection problems.

• Rec.puzzles archive: coloring problems.

• Rectangles divided into (mostly) unequal squares, R. W. Gosper.

• Rectangular cartograms: the game. Change the shape of rectangles (without changing their area) and group them into larger rectangular and L-shaped units to fit them into a given frame. Bettina Speckmann, TUE. Requires a browser with support for Java SE 6.

• The reflection of light rays in a cup of coffee or the curves obtained with b^n mod p, S. Plouffe, Simon Fraser U. (Warning: large animated gif. You may prefer the more wordy explanation at Plouffe's other page on the same subject.)

• Reuleaux triangles. These curves of constant width, formed by combining three circular arcs into an equilateral triangle, can drill out (most of) a square hole.
  

• Rhombic tilings. Abstract of Serge Elnitsky's thesis, "Rhombic tilings of polygons and classes of reduced words in Coxeter groups". He also supplied the picture below of a rhombically tiled 48-gon, available with better color resolution from his website.
  

• Rigid regular r-gons. Erich Friedman asks how many unit-length bars are needed in a bar-and-joint linkage network to make a unit regular polygon rigid. What if the polygon can have non-unit-length edges?
  

• The rotating caliper graph. A thrackle used in "Average Case Analysis of Dynamic Geometric Optimization" for maintaining the width and diameter of a point set.
  

• Russian math olympiad problem on lattice points. Proof that, for any five lattice points in convex position, another lattice point is on or inside the inner pentagon of the five-point star they form.
  

• Secrets of Da Vinci's challenge. A discussion of the symbology and design of this interlocked-circle-pattern puzzle.

• Semi-regular tilings of the plane, K. Mitchell, Hobart and William Smith Colleges.

• Sensitivity analysis for traveling salesmen, C. Jones, U. Washington. Still a good title, and now the geometry has been made more entertaining with Java and VRML.

• Sets of points with many halving lines. Coordinates for arrangements of 14, 16, and 18 points for which many of the lines determined by two points split the remaining points exactly in half. From my 1992 tech. report.

• Seven circle theorem, an applet illustrating the fact that if six circles are tangent to and completely surrounding a seventh circle, then connecting opposite points of tangency in pairs forms three lines that meet in a single point, by Michael Borcherds. Other applets by Borcherds include Poncelet's porism, a similar porism with an ellipse and a parabola and with two ellipses, and more generally with two conics of variable type.

• 75-75-30 triangle dissection. This isosceles triangle has the same area as a square with side length equal to half the triangle's long side. Ed Pegg asks for a nice dissection from one to the other.

• Sierpinski carpet on the sphere. From Curtis McMullen's math gallery.

• Sierpinski triangle reptile based on a complex binary number system, R. W. Gosper.

• Sierpinski valentine from XKCD.

• Sighting point. John McKay asks, given a set of co-planar points, how to find a point to view them all from in a way that maximizes the minimum viewing angle between any two points. Somehow this is related to monodromy groups. I don't know whether he ever got a useful response. This is clearly polynomial time: the decision problem can be solved by finding the intersection of O(n²) shapes, each the union of two disks, so doing this naively and applying parametric search gives O(n⁴ polylog), but it might be interesting to push the time bound further. A closely related problem of smoothing a triangular mesh by moving points one at a time to optimize the angles of incident triangles can be solved in linear time by LP-type algorithms [Matousek, Sharir, and Welzl, SCG 1992; Amenta, Bern, and Eppstein, SODA 1997].

• Simple polygonizations. Erik Demaine explores the question of how many different non-crossing traveling salesman tours an n-point set can have.

• Smarandache Manifolds online e-book by Howard Iseri. I'm not sure I see why this should be useful or interesting, but the idea seems to be to define geometry-like structures (having objects called points and lines that somehow resemble Euclidean points and lines) that are non-uniform in some strong sense: every Euclidean axiom (and why not, every Euclidean theorem?) should be true at some point of the geometry and false at some other point.

• The smoothed octagon. A candidate for the symmetric convex shape that is least able to pack the plane densely.

• Smoothly rolling polygonal wheels and their roads, H. Serras, Ghent.

• Snakes. What is the longest path of unit-length line segments, connected end-to-end with angles that are multiples of some fixed d, and that can be covered by a square of given size?

• sneJ made a Mandelbrot set with sheet plastic and a laser cutter.

• Snowflake reptile hexagonal substitution tiling (sometimes known as the Gosper Island) rediscovered by NASA and conjectured to perform visual processing in the human brain.

• Soap films and grid walks, Ivar Peterson. A discussion of Steiner tree problems in rectilinear geometry.

• Soddy Spiral. R. W. Gosper calculates the positions of a sequence of circles, each tangent to the three previous ones.

• Sofa movers' problem. This well-known problem asks for the largest area of a two-dimensional region that can be moved through a hallway with a right-angled bend. Part of Mathsoft's collection of mathematical constants.

• Some generalizations of the pinwheel tiling, L. Sadun, U. Texas.

• Spidron, a triangulated double spiral shape tiles the plane and various other surfaces. With photos of related paperfolding experiments.

• Spira Mirabilis logarithmic spiral applet by A. Bogomily.

• Spiral generator, web form for creating bitmap images of colored logarithmic spirals.
  

• Spiral in a liquid crystal film.

• Spiral tilings. These similarity tilings are formed by applying the exponential function to a lattice in the complex number plane.
  

• Spiral triangles, Eric Weeks.

• Spirals. Mike Callahan and Larry Shook use a spreadsheet to investigate the spirals formed by repeatedly nesting squares within larger squares.

• Spirals and other 2d curves, Jan Wassenaar.

• Split square. How to subdivide a square into two rectangular pieces, one of which circumscribes the other?
  

• sqfig and sqtile, software by Eric Laroche for generating polyominoes and polyomino tilings.

• Squared squares and squared rectangles, thorough catalog by Stuart Anderson. Erich Friedman discusses several related problems on squared squares: if one divides a square into k smaller squares, how big can one make the smallest square? How small can one make the biggest square? How few copies of the same size square can one use? See also Robert Harley's four-colored squared square, Mathworld's perfect square dissection page, a Geometry Forum problem of the week on squared squares, Keith Burnett's perfect square dissection page, and Bob Newman's squared square drawing.

• Squares on a Jordan curve. Various people discuss the open problem of whether any Jordan curve in the plane contains four points forming the vertices of a square, and the related but not open problem of how to place a square table level on a hilltop. This is also in the geometry.puzzles archive.

• Stomachion, a tangram-like shape-forming game based on a dissection of the square and studied by Archimedes.

• Wilson Stothers' Cabri pages. Geometric animations teaching projective conics, hyperbolic geometry, and the Klein view of geometry as symmetry.

• Straighten these curves. This problem from Stan Wagon's PotW archive asks for a dissection of a circle minus three lunes into a rectangle. The ancient Greeks performed similar constructions for certain lunules as an approach to squaring the circle.

• Supershapes and 3d supershapes. Paul Bourke generates a wide variety of interesting shapes from a simple formula. See also John Whitfield's Nature article.

• Sylvester's theorem. This states that any finite non-colinear point set has a line containing only two points (equivalently, every zonohedron has a quadrilateral face). Michael Larsen, Tim Chow, and Noam Elkies discuss two proofs and a complex-number generalization. (They omit the very simple generalization from Euler's formula: every convex polyhedron has a face of degree at most five.)

• SymmeToy, windows shareware for creating paint patterns, symmetry roses, tessellated art and symmetrically decorated 3D polyhedron models.

• Symmetry and Tilings. Charles Radin, Not. AMS, Jan. 1995. See also his Symmetry of Tilings of the Plane, Bull. AMS 29 (1993), which proves that the pinwheel tiling is ergodic and can be generated by matching rules.

• Symmetry in Threshold Design in South India.

• Tangencies. Animated compass and straightedge constructions of various patterns of tangent circles.
  

• Tangencies of circles and spheres. E. F. Dearing provides formulae for the radii of Apollonian circles, and analogous three-dimensional problems.

• Thrackles are graphs embedded as a set of curves in the plane that cross each other exactly once; Conway has conjectured that an n-vertex thrackle has at most n edges. Stephan Wehner describes what is known about thrackles.

• 3d-XplorMath Macintosh software for visualizing curves, surfaces, polyhedra, conformal maps, and other planar and three-dimensional mathematical objects.

• Three spiral tattoos from the Discover Magazine Science Tattoo Emporium.

• Tic tac toe theorem. Bill Taylor describes a construction of a warped tic tac toe board from a given convex quadrilateral, and asks for a proof that the middle quadrilateral has area 1/9 the original. Apparently this is not even worth a chocolate fish.

• Tiling problems. Collected at a problem session at Smith College, 1993, by Marjorie Senechal.

• Tiling a rectangle with the fewest squares. R. Kenyon shows that any dissection of a p*q rectangle into squares (where p and q are integers in lowest terms) must use at least log p pieces.

• Tiling transformer. Java applet for subdividing tilings (starting from a square or hexagonal tiling) in various different ways.
  

• Tiling the unit square with rectangles. Erich Friedman shows that the 5/6 by 5/6 square can always be tiled with 1/(k+1) by 1/(k+1) squares. Will all the 1/k by 1/(k+1) rectangles, for k>0, fit together in a unit square? Note that the sum of the rectangle areas is 1. Marc Paulhus can fit them into a square of side 1.000000001: "An algorithm for packing squares", J. Comb. Th. A 82 (1998) 147-157, MR1620857.

• Tilings. Lecture notes from the Clay Math Institute, by Richard Stanley and Federico Ardila, discussing polyomino tilings, coloring arguments for proving the nonexistence of tilings, counting how many tilings a region has, the arctic circle theorem for domino tilings of diamonds, tiling the unit square with unit-fraction rectangles, symmetry groups, penrose tilings, and more. In only 21 pages, including the annotated bibliography. A nice but necessarily concise introduction to the subject. (Via Andrei Lopatenko.)

• Tim's Triangular Page.

• Totally Tessellated. Mosaics, tilings, Escher, and beyond.

• Transformational geometry. Leslie Howe illustrates various plane symmetry types with Cabri animations.

• Traveling salesman problem and Delaunay graphs. Mike Dillencourt and Dan Hoey revisit and simplify some older work showing that the traveling salesman tour of a point set need not follow Delaunay edges.

• Triangle centers.

• Triangle geometry and the triangle book. Steve Sigur's web site describing many important triangle centers and loci. According to the site, he also has a book with John Conway on the subject, coming soon.

• Triangle tiling. Geom. Ctr. exhibit at the Science Museum of Minnesota.

• Triangulated pig. M. Bern, Xerox.

• Triangulations and arrangements. Two lectures by Godfried Toussaint, transcribed by Laura Anderson and Peter Yamamoto. I only have the lecture on triangulations.

• Triangulations with many different areas. Eddie Grove asks for a function t(n) such that any n-vertex convex polygon has a triangulation with at least t(n) distinct triangle areas, and also discusses a special case in which the vertices are points in a lattice.

• Trisecting an angle with origami. Julie Rehmeyer, MathTrek.

• Typeface Venus, Circle Marilyn, and Bubble Mona. village9991 uses quadtrees and superellipses to make abstract mosaics of famous faces.

• Tysen loves hexagons. And supplies ascii, powerpoint, and png graphics for several styles of hexagonal grid graph paper.

• Uniqueness of focal points. A focal point (aka equichord) in a star-shaped curve is a point such that all chords through the point have the same length. Noam Elkies asks whether it is possible to have more than one focal point, and Curtis McMullen discusses a generalization to non-star-shaped curves. This problem has recently been put to rest by Marek Rychlik.

• Universal coverage constants. What is the minimum area figure of a given type that covers all unit-diameter sets? Part of Mathsoft's collection of mathematical constants.

• Untitled, Forbes Gallery, 1987, Ken Goldberg.

• A Venn diagram made from five congruent ellipses. From F. Ruskey's Combinatorial Object Server.
  

• Voronoi Art. Scott Sona Snibbe uses a retro-reflective floor to display the Voronoi diagram of people walking on it, exploring notions of personal space and individual-group relations. Additional Voronoi-based art is included in his dynamic systems series.

• Voronoi diagrams at the Milwaukee Art Museum. Scott Snibbe's artwork Boundary Functions, as blogged by Quomodumque.

• Voronoi diagrams of lattices. Greg Kuperberg discusses an algorithm for constructing the Voronoi cells in a planar lattice of points. This problem is closely related to some important number theory: Euclid's algorithm for integer GCD's, continued fractions, and good approximations of real numbers by rationals. Higher-dimensional generalizations (in which the Voronoi cells form zonotopes) are much harder -- one can find a basis of short vectors using the well-known LLL algorithm, but this doesn't necessarily find the vectors corresponding to Voronoi adjacencies. (In fact, according to Senechal's Quasicrystals and Geometry, although the set of Voronoi adjacencies of any lattice generates the lattice, it's not known whether this set always contains a basis.)

• Voronoi diagrams and ornamental design.

• The Voronoi Game. Description, articles, references, and demonstration applet on problems of competitive facility location, where two players place sites in hopes of being nearest to as much area as possible. See also Crispy's Voronoi game applet and Dennis Shasha's Voronoi game page.

• Wallpaper groups. An illustrated guide to the 17 planar symmetry patterns. See also Xah Lee's wallpaper group page.

• Wallpaper patterns, R. Morris. Kaleidoscope-like Java applet for making and transforming symmetric tilings out of uploaded photos.

• What happens when you connect uniformly spaced but not dyadic rational points along the Peano spacefilling curve? R. W. Gosper illustrates the results.
  

• What is arbelos you ask?

• Worm in a box. Emo Welzl proves that every curve of length pi can be contained in a unit area rectangle.

• WWW spirograph. Fill in a form to specify radii, and generate pictures by rolling one circle around another. For more pictures of cycloids, nephroids, trochoids, and related spirograph shapes, see David Joyce's Little Gallery of Roulettes. Anu Garg has implemented spirographs in Java.

• yukiToy. Shockwave plugin software for pushing around a few reddish spheres in your browser window. But what exactly is the point? (They're spheres, they don't have one, I guess.)

• Zef Damen Crop Circle Reconstructions. What is the geometry underlying the construction of these large-scale patterns?

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein, Theory Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file.