My Own Contributions to the Junkyard

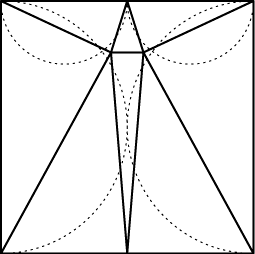
• Acute square triangulation. Can one partition the square into triangles with all angles acute? How many triangles are needed, and what is the best angle bound possible?

  

• Algorithms for coloring quadtrees.

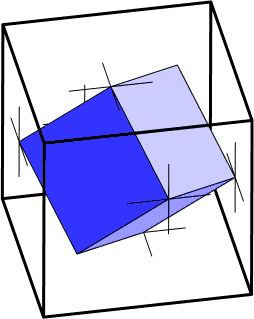
• Box in a box. What is the smallest cube that can be put inside another cube touching all its faces? There is a simple solution, but it seems difficult to prove its correctness. The solution and proof are even prettier in four dimensions.

  

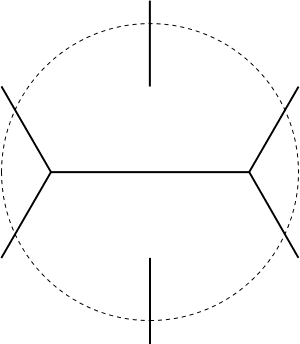
• Building a better beam detector. This is a set that intersects all lines through the unit disk. The construction below achieves total length approximately 5.1547, but better bounds were previously known.

  

• Carnival triangles. A factoid about similar triangles inspired by a trigonometric identity.

• Centers of maximum matchings. Andy Fingerhut asks, given a maximum (not minimum) matching of six points in the Euclidean plane, whether there is a center point close to all matched edges (within distance a constant times the length of the edge). If so, it could be extended to more points via Helly's theorem. Apparently this is related to communication network design. I include a response I sent with a proof (of a constant worse than the one he wanted, but generalizing as well to bipartite matching).

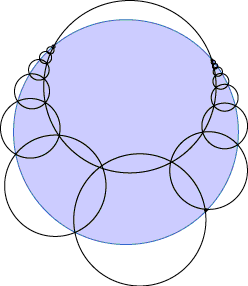
• Circular coverage constants. How big must N equal disks be in order to completely cover the unit disk? What about disks with sizes in geometric progression? From MathSoft's favorite constants pages.

  

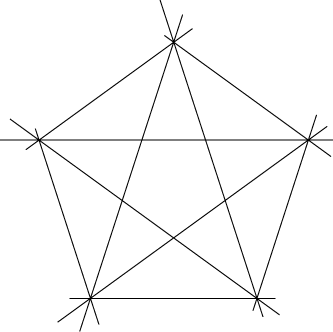
• Coloring line arrangements. The graphs formed by overlaying a collection of lines require three, four, or five colors, depending on whether one allows three or more lines to meet at a point, and whether the lines are considered to wrap around through infinity. Stan Wagon asks similar questions for unit circle arrangements.

  

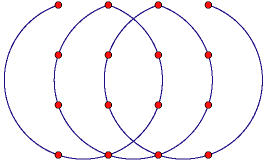
• Connect the dots. Ed Pegg asks how many sides are needed in a (self-crossing) polygon, that passes through every point of an n*n grid. I added a similar puzzle with circular arcs.

  

• Dilation-free planar graphs. How can you arrange n points so that the set of all lines between them forms a planar graph with no extra vertices?

  

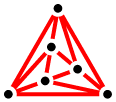
• Dissection and dissection tiling. This page describes problems of partitioning polygons into pieces that can be rearranged to tile the plane. (With references to publications on dissection.)

  

• Do buckyballs fill hyperbolic space?

• Edge-tangent polytope illustrating Koebe's theorem that any planar graph can be realized as the set of tangencies between circles on a sphere. Placing vertices at points having those circles as horizons forms a polytope with all edges tangent to the sphere. Rendered by POVray.

  

• Equilateral triangles. Dan Asimov asks how large a triangle will fit into a square torus; equivalently, the densest packing of equilateral triangles in the pattern of a square lattice. There is only one parameter to optimize, the angle of the triangle to the lattice vectors; my answer is that the densest packing occurs when this angle is 15 or 45 degrees, shown below. (If the lattice doesn't have to be square, it is possible to get density 2/3; apparently this was long known, e.g. see Fáry, Bull. Soc. Math. France 78 (1950) 152.)

  Asimov also asks for the smallest triangle that will always cover at least one point of the integer lattice, or equivalently a triangle such that no matter at what angle you place copies of it on an integer lattice, they always cover the plane; my guess is that the worst angle is parallel and 30 degrees to the lattice, giving a triangle with 2-unit sides and contradicting an earlier answer to Asimov's question.

  

• Flat equilateral tori. Can one build a polyhedral torus in which all faces are equilateral triangles and all vertices have six incident edges? Probably not but this physical model comes close.

  

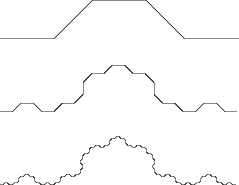
• A fractal beta-skeleton with high dilation. Beta-skeletons are graphs used, among other applications, in predicting which pairs of cities should be connected by roads in a road network. But if you build your road network this way, it may take you a long time to get from point a to point b.

  

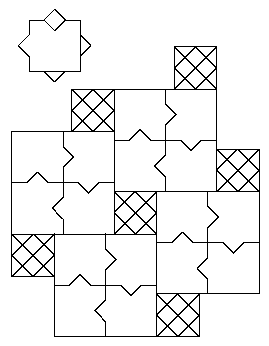
• Heesch's problem. How many times can a shape be completely surrounded by copies of itself, without being able to tile the entire plane? W. R. Marshall and C. Mann have recently made significant progress on this problem using shapes formed by indenting and outdenting the edges of polyhexes.

  

• Hinged dissections of polyominoes

  

• Hinged kite mirror dissection. General techniques for cutting any polygon into pieces that can be unfolded and refolded to form the polygon's mirror image.

  

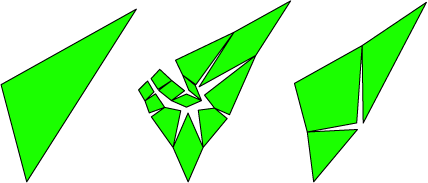
• Infinite families of simplicial arrangements.

  

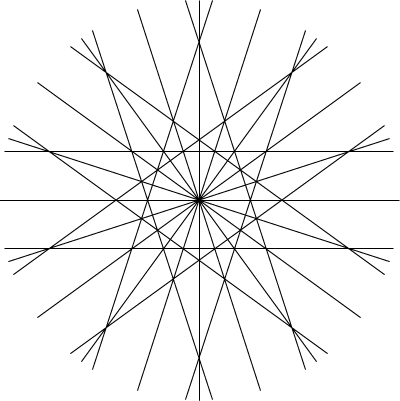
• Labyrinth tiling. This aperiodic substitution tiling by equilateral and isosceles triangles forms fractal space-filling labyrinths.

  

• Lattice pentagons. The vertices of a regular pentagon are not the subset of any lattice.

• Layered graph drawing.

  

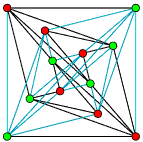
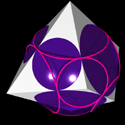
• Miquel's six circles in 3d. Reinterpreting a statement about intersecting circles to be about inscribed cuboids.

  

• My face on a Voronoi Diagram.

• Origamic tetrahedron. The image below depicts a way of making five folds in a 2-3-4 triangle, so that it folds up into a tetrahedron. Toshi Kato asks if you can fold the triangle into a tetrahedron with only three folds. It turns out that there is a unique solution, although many tetrahedra can be formed with more folds.

  

• Paraboloid. Ray-traced image created to illustrate the lifting transformation used to relate Delaunay triangulation with convex hulls in one higher dimension.

  

• Proofs of Euler's Formula. V-E+F=2, where V, E, and F are respectively the numbers of vertices, edges, and faces of a convex polyhedron.

• Pushing disks together. If unit disks move so their pairwise distances all decrease, does the area of their union also decrease?

• Quicktime VR and mathematical visualization.

• The rotating caliper graph. A thrackle used in "Average Case Analysis of Dynamic Geometric Optimization" for maintaining the width and diameter of a point set.

  

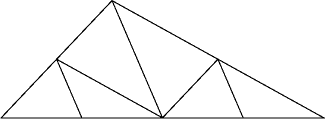
• Russian math olympiad problem on lattice points. Proof that, for any five lattice points in convex position, another lattice point is on or inside the inner pentagon of the five-point star they form.

  

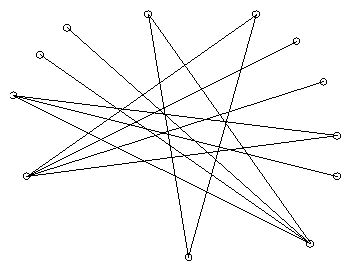
• Sets of points with many halving lines. Coordinates for arrangements of 14, 16, and 18 points for which many of the lines determined by two points split the remaining points exactly in half. From my 1992 tech. report.

• 75-75-30 triangle dissection. This isosceles triangle has the same area as a square with side length equal to half the triangle's long side. Ed Pegg asks for a nice dissection from one to the other.

• Sliced ball. Ray-traced image created to help describe recent algorithms for removing slivers from tetrahedral meshes.

  

• Spiral tilings. These similarity tilings are formed by applying the exponential function to a lattice in the complex number plane.

  

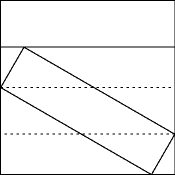
• Split square. How to subdivide a square into two rectangular pieces, one of which circumscribes the other?

  

• Symmetries of torus-shaped polyhedra

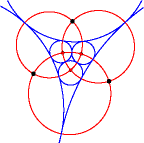
• Tangencies. Animated compass and straightedge constructions of various patterns of tangent circles.

  

• The tea bag problem. How big a volume can you enclose by two square sheets of paper joined at the edges? See also the cubical teabag problem.

• Tetrahedra classified by their bad angles. From "Dihedral bounds for mesh generation in high dimensions".

  

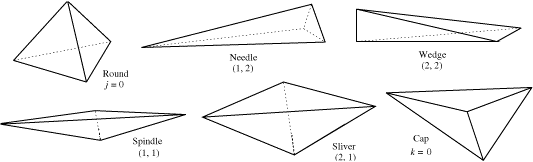
• Three untetrahedralizable objects

     

• Triangles and squares. Slides from a talk I gave relating a simple 2d puzzle, Escher's drawings of 3d polyhedra, and the combinatorics of 4d polytopes, via angles in hyperbolic space. Warning: very large file (~8Mb). For more technical details see my paper with Kuperberg and Ziegler.

  

• Triangulating 3-dimensional polygons. This is always possible (with exponentially many Steiner points) if the polygon is unknotted, but NP-complete if no Steiner points are allowed. The proof uses gadgets in which quadrilaterals are stacked like Pringles to form wires.

  

• Ukrainian Easter Egg. This zonohedron, computed by a Mathematica notebook I wrote, provides a lower bound for the complexity of the set of centroids of points with approximate weights.

  

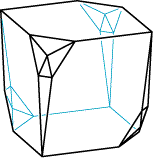
• An uninscribable 4-regular polyhedron. This shape can not be drawn with all its vertices on a single sphere.

  

• Zonohedra and cubic partial cubes. Connecting the geometric problem of classifying simplicial line arrangements to the graph-theoretic one of finding regular graphs that can be isometrically embedded on a cube.